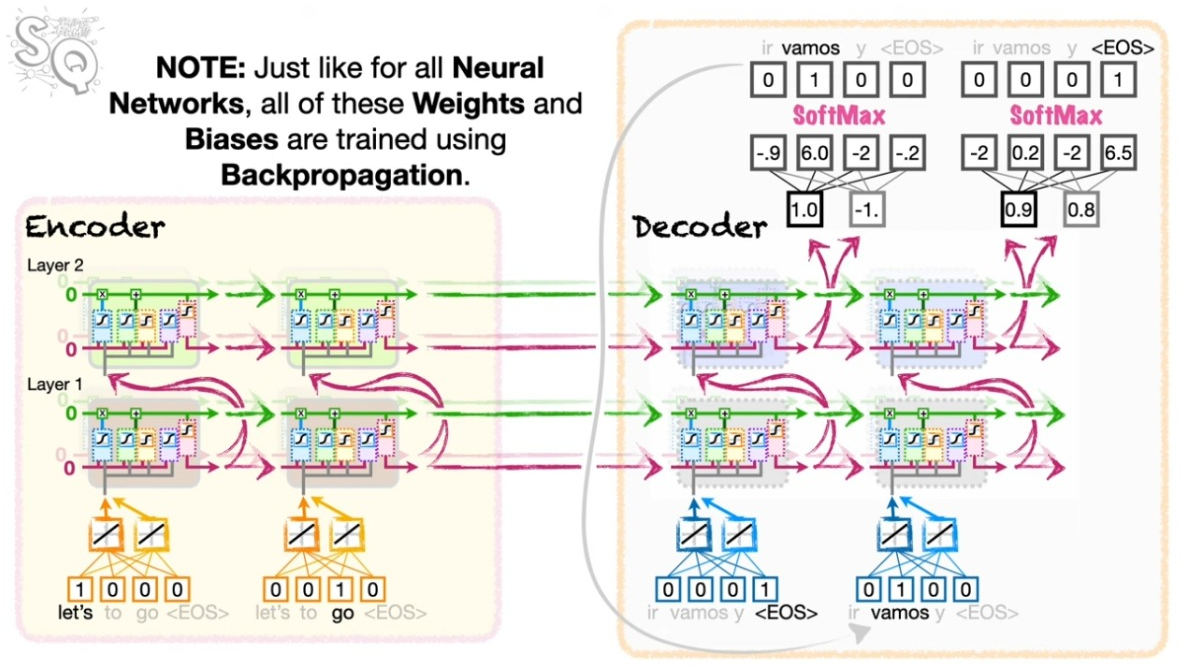
Attention Model
TL; DR
어텐션을 반영하는 하나의 방법을 살펴보자.
넋두리
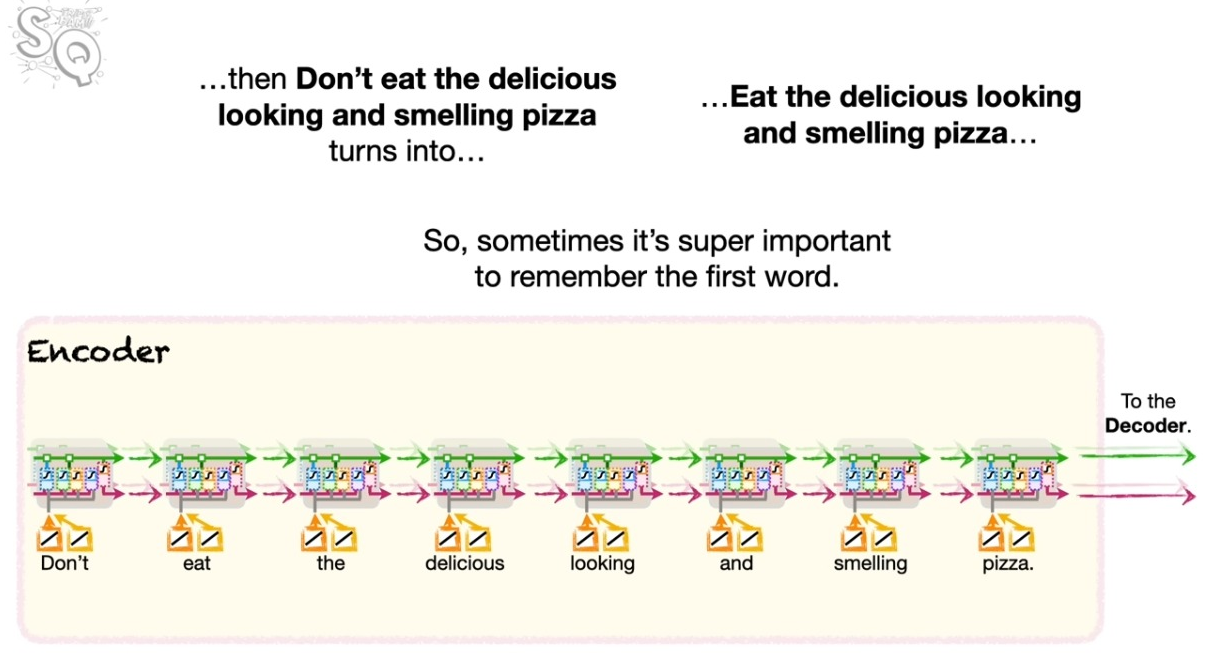
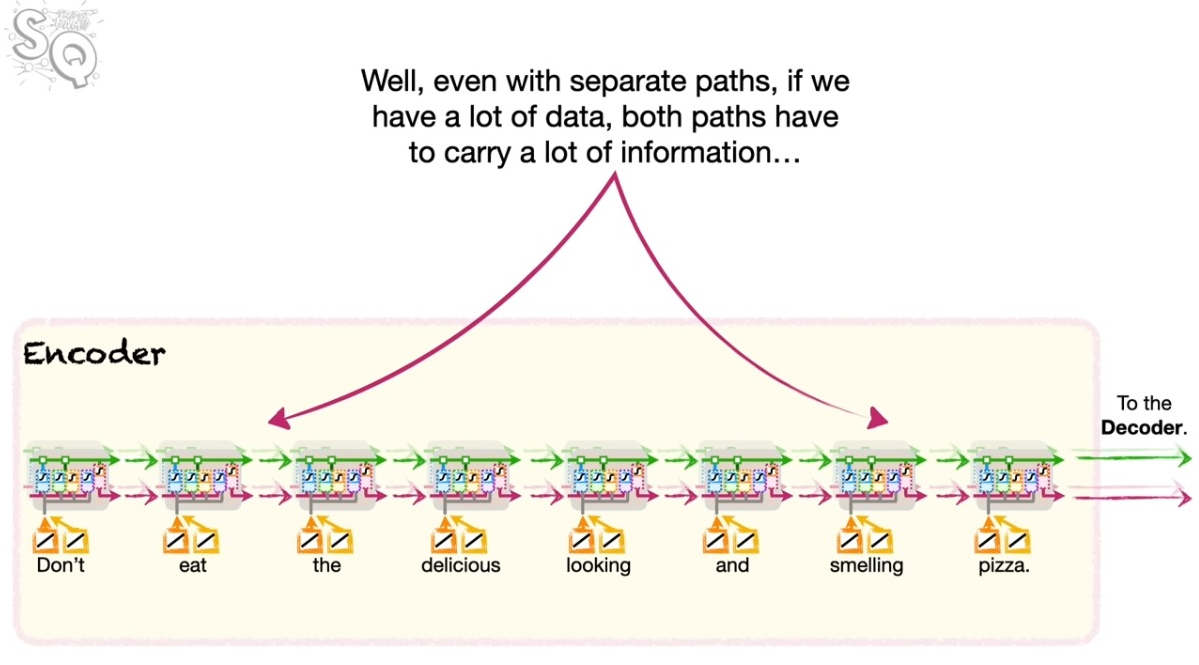
LSTM은 단기와 장기의 기억을 나눠서 전달함으로써 RNN이 지는 문제점을 극복하고자 했다. 하지만 여전히 남는 문제가 있었으니, 언어에 따라서 혹은 표현에 따라서 거리가 많이 떨어지는 정보값이 중요해지는 경우가 종종 존재한다.
아래의 그림을 보자.
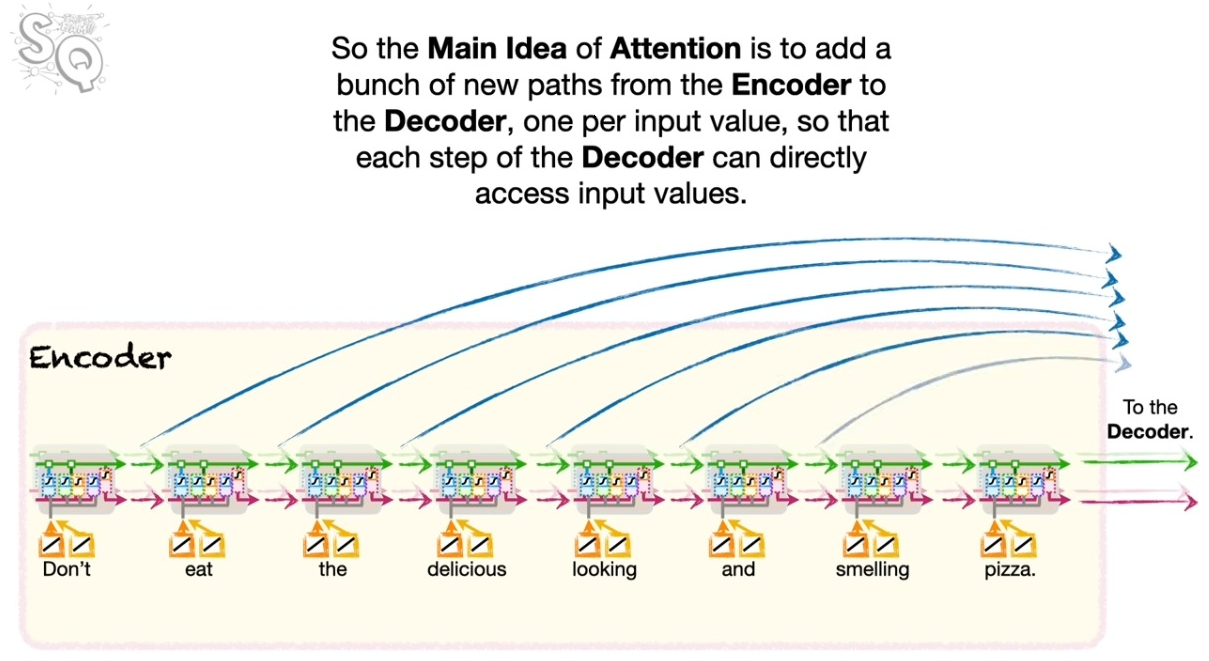
어텐션이란 무엇인가?
인코더-디코더 모델을 생각해보자. 결국 인코더의 특정 정보와 디코더의 특정 정보가 얼마나 비슷한지가 문제의 핵셤이다. 만일 둘이 비슷하다면 생성에서 이를 더 강하게 반영하는 것이 맞을 것이다. 인코딩에서 강조된 내용이 디코딩에서도 강조되도록 해야 한다.
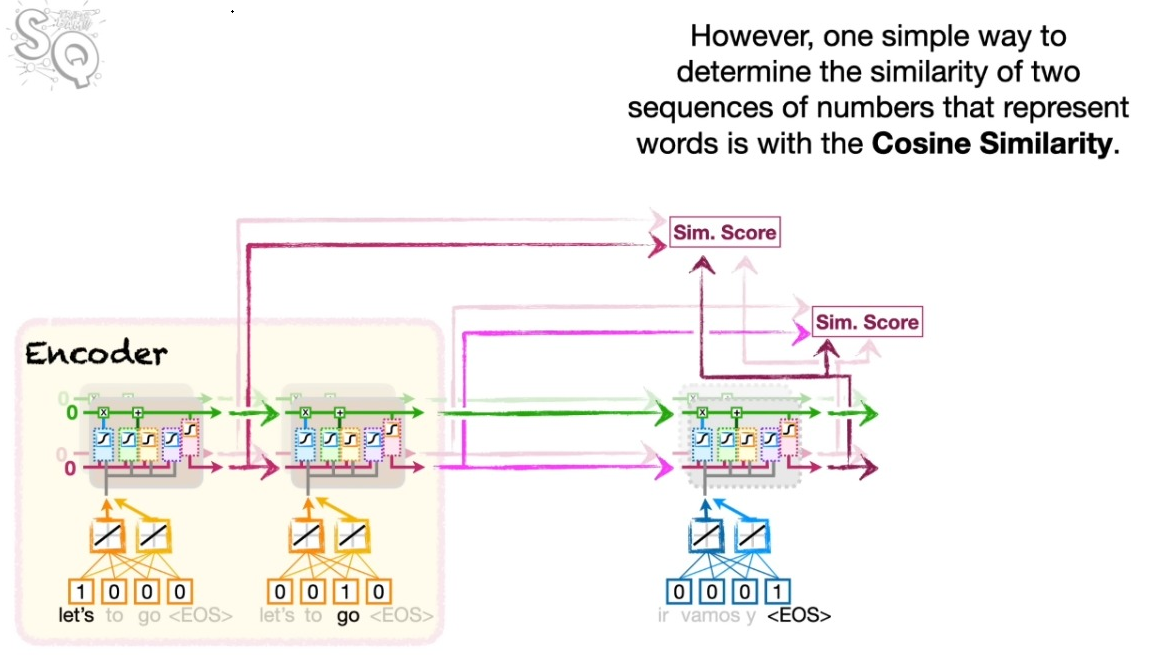
핵심은 인코딩과 디코딩 정보의 유사성을 측정하는 데 있다. 측정에는 여러가지 방법이 있을 것인데, 강의에서는 코사인 유사도를 사용한다. 우리는 벡터를 다루고 있고 두 벡터 사이의 비슷한 정도를 측정하는 데에는 코사인 유사도만한 것이 없다.
코사인 유사도 대신 닷 프로덕트
코사인 유사도의 원래 정의는 다음과 같다. 크기가 같은 벡터 \(a_i\), \(b_i\)가 있다고 하자.
\[ \text{Cosine Similarity} = \dfrac{\sum_{i=1}^n a_i b_i}{\sqrt{\sum_{i=1}^n a_i^2} \sqrt{\sum_{i=1}^n b_i^2}} \]
식에서 분모는 위의 닷 프로덕트(내적)의 크기를 조절해주는 역할이다. 이 덕분에 코사인 유사도는 그 이름에 걸맞게 \([-1, 1]\) 사이의 값을 지니게 된다. 스케일링이 필요한 이유는 개별 벡터의 값이 닷 프로덕트에서 지니게 되는 값의 효과를 통제하기 위해서다. 그런데 앞에서 보듯이 LSTM의 경우에는 산출되는 벡터의 값이 \([-1,1]\)사이를 벗어날 수 없다. 따라서 분모는 무시하고 분자만 다루도록 하자.
어텐션 구현하기
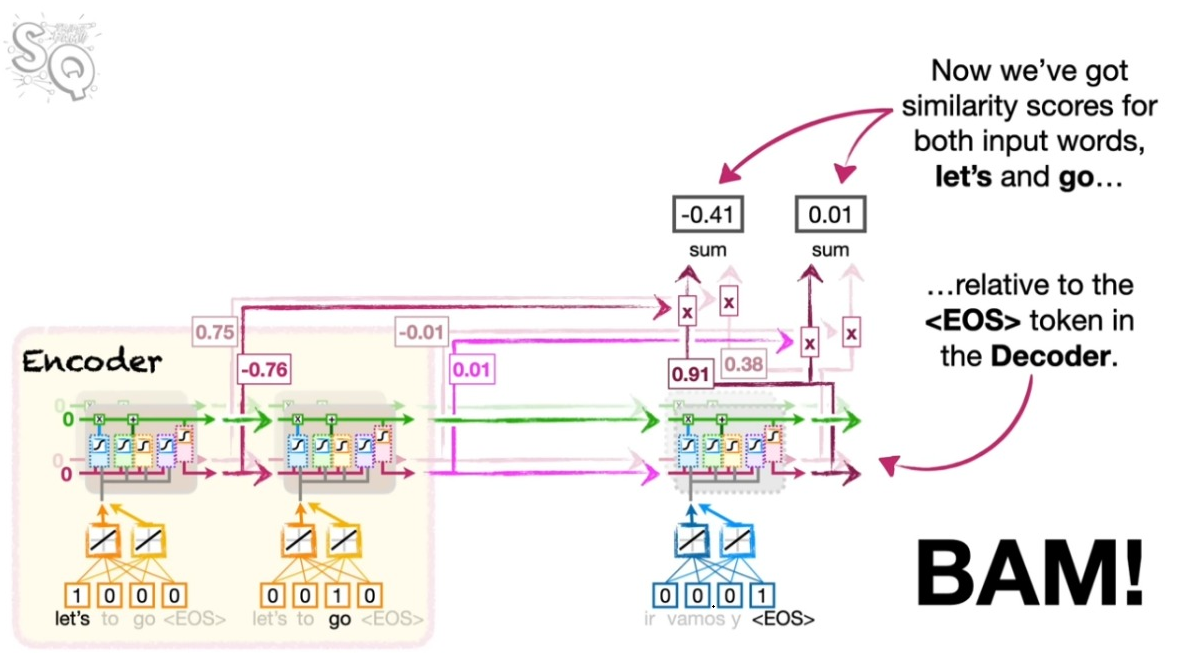
아래 왼쪽 그림을 보자. 인코더의 첫번째 셀의 벡터와 디코더의 첫번째 셀의 결과의 코사인 유사도를 먼저 후간다. 같은 방식으로 두번째 셀의 벡터와 디코더의 첫번째 셀의 결과의 코사인 유사도를 구한다.
오른쪽 그림처럼 이렇게 구한 코사인 유사도가 일정의 어텐션의 지표가 된다.
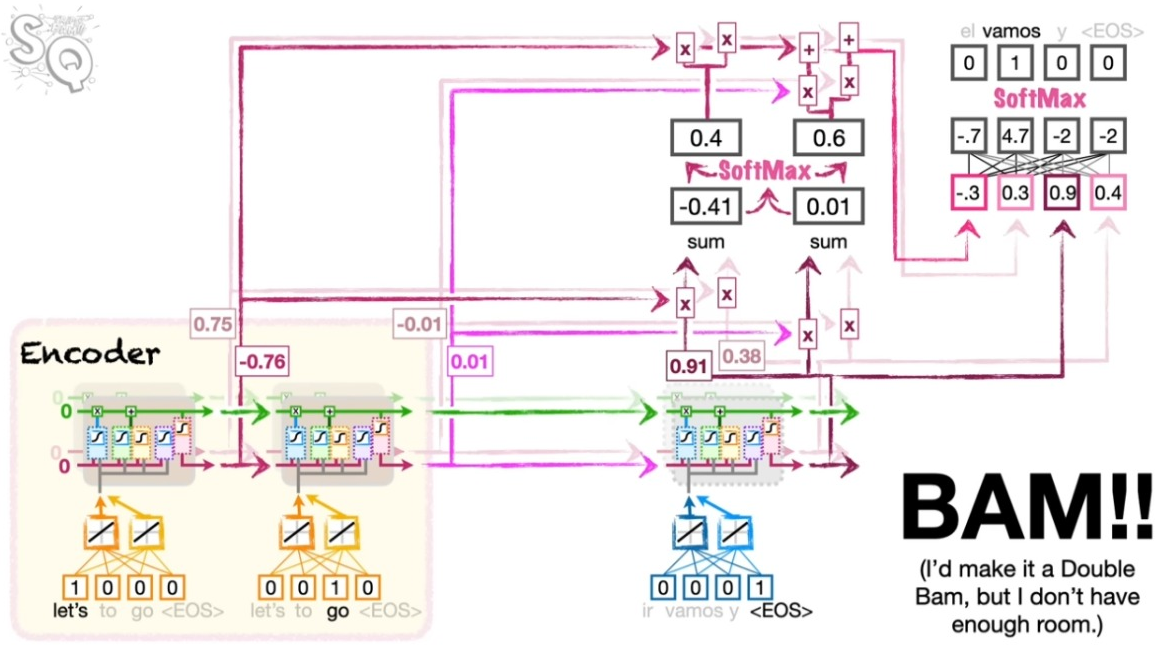
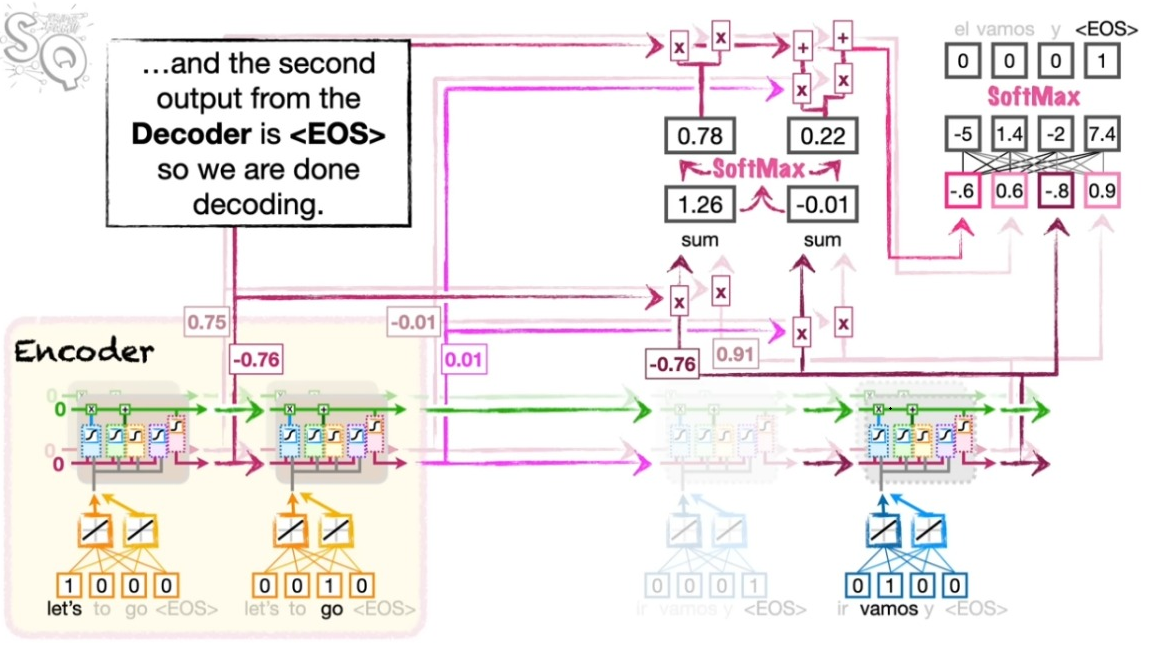
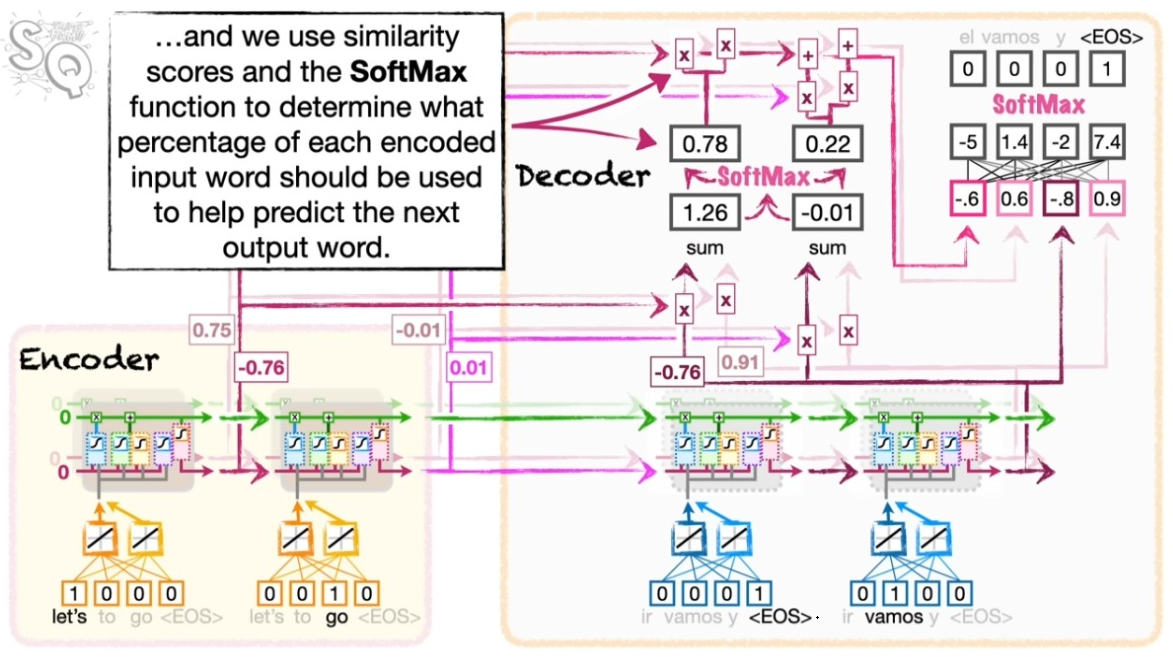
이제 이렇게 확보된 어텐션 지표가 디코딩에서 직접 활용된다. 해당 지표를 소프트맥스 처리하고 이를 다시 인코더의 정보와 결합한 뒤 스페인 어로 풀어 놓는다. 여기서 소프트맥스 처리된 코사인 유사도는 인코더의 정보를 어느 정도의 비중으로 반영해야 하는지를 결정한다. 물론 앞서와 마찬가지로 <EOS>가 산출될 때까지 이 과정을 반복한다.
Seq2Seq 모델과 비교하기
아래 그림에서 보듯이 Seq2Seq 모델에 비해서 인코딩의 정보가 디코딩에 직접적으로 영향을 끼치는 것을 알 수 있다.