Sample Statistics and Standard Error
\[ \def\E{{\mathbb E}} \def\V{{\mathbb V}} \def\ES#1{\overline{#1}} \]
TL; DR
- 기본 통계학 용어와 개념 몇 개를 두서없이 내 맘대로 정리한다.
- 자주 잊는 나를 위한 개인적인 용도
Why
통계학을 배운 사람들이라면 표준 오차는 대체로 잘 아는 내용이다. 그런데 나는 가끔 까먹는다. 개인적인 용도를 위해서 관련된 앞뒤 내용 몇 가지를 순서 없이 정리해둔다.
Big Ifs
- 알려진 파라미터는 없다.
- 알려진 분포도 없다.
- 표본은 평균이 \(\mu\)이고 분산이 \(\sigma^2 < \infty\)인 분포에서 IID(independent and identically distributed)로 추출된다.
Finite Sample vs Asymptotic Properties
“유한 표본 finite sample”이란 어떤 크기든 표본의 크기가 정해져 있다는 의미이다. 가끔 “소 표본 small sample”이라는 표현도 활용된다. “점근적 특성 asymptotic properties”이란 표본 크기가 계속 커질 때 추정량이 지니는 특성을 의미한다. 통계학을 배울 때는 유한 표본의 추정량(estimator)에 관해 먼저 엄밀하게 배운다. 통계학을 활용한다는 실용적인 관점에서 중요한 것은 추정량의 점근적 특징이다.
점근성에 관해서 두 가지를 짚고 가자. 일치성은 샘플의 크기가 커질수록 추정량이 모수에 접근하는 특징이다. 다른 하나는 중심 극한 정리(central limit theorem)이다. 샘플의 크기가 커질수록 추정량의 분포가 정규 분포에 접근하게 된다. 일치성이 확보되면 추정량이 불편성을 지니고 있지 않아도 표본의 크기가 커질수록 참값에 충분히 가깝게 접근한다. 한편 중심 극한 정리는 추정량의 통계적인 검정을 위한 매우 중요한 방법을 제공한다. 아래에서 다시 살펴보기로 하자.
Unbiasedness, Efficiency, Consistency
파라미터 \(\theta\)와 이 모수에 관한 추정량 \(\hat \theta\)이 있다고 하자.
표본 \(x_i\)가 있다고 할 때, \(\hat \theta\)는 표본 \(x_i\)라는 정보를 통해 구성된다. 즉, \(\hat\theta \equiv \hat\theta(x_i)\).
Unbiased \[ \E(\hat \theta) = \theta \]
불편성은 추정량의 중요한 특징이지만, 불편성만으로 충분하지 않다. 극단적인 예로 \(X\)에서 추출된 샘플 하나를 \(x_1\)라고 하자. 이 샘플 하나를 추정량으로 쓰면 이 역시 불편성을 지니고 있다 (\(\E(x_1) = \theta\)). 하지만 이 추정량은 좋은 추정량이 아니다.
Efficiency
\(\theta\)에 대해서 \(\hat \theta_1\)과 \(\hat \theta_2\) 두 개의 추정량이 있다고 하자. \[ \rm{Var} (\hat\theta_1) \leq \rm{Var} (\hat\theta_2) \]
모든 \(\theta\)에 대해서 위의 부등식이 성립하고, 적어도 하나의 \(\theta\)에 대해서 강 부등호가 성립하면 \(\hat\theta_1\)이 \(\hat\theta_2\)보다 효율적이다.
Consistent
표본의 크기에 따른 추정량의 시퀀스 \(\lbrace \hat\theta_n \rbrace\)이 있다고 할 때, \[ \underset{n \to \infty}{\rm plim}~\hat\theta_n = \theta \]
plim의 정의는 다음과 같다. 표본 크기 \(n\)과 임의의 양의 상수 \(c\)에 대하여 표본 추정량 \(\hat\theta_n\)은 \(\theta\)의 일치 추정량(consistent estimator)이라고 한다.
\[ \lim_{n\to\infty}P[|\hat\theta_n - \theta|\geq c]=0 \]
Concepts
| 용어 | 영어 표현 | 정의 | 사례 혹은 코멘트 |
|---|---|---|---|
| 모수 | parameter | 한 모집단의 고정된 특성 혹은 이를 나타내는 값 | \(\E[Y_i]\), 분포의 \(\mu\), \(\sigma^2\) |
| 표본 통계량 | sample statistics | 표본에 따라서 변화하는 값 | \(\ES{Y}_n\), \(S(Y_i)^2\), \(SE\), \(\widehat{SE}\) |
| 표본 평균 | sample mean | 표본의 평균 | \(\ES{Y}_n = \frac{1}{n}\sum_{i=1}^n Y_i\) |
| 표본 분산 | sample variance | 표본의 분산 | \(S(Y_i)^2 = \frac{1}{n-1}\sum_{i=1}^n (Y_i - \ES{Y}_n)^2\) |
| 표준 오차 | standard error | 표본 통계량의 표준 편차 | \(SE(\ES{Y}_n) = \frac{\sigma_Y}{\sqrt{n}}\) |
| 표준 오차의 추정치 | estimated standard error | 표준 오차 계산 시 \(\sigma_Y \to S(Y_i)\) | \(\widehat{SE}(\ES{Y}_n) = \frac{S(Y_i)}{\sqrt{n}}\) |
| \(t-\)통계량 | \(t-\)statistic | \(t(\mu) = \frac{\ES{Y}_n - \mu}{\widehat{SE}(\ES{Y}_n)}\) | \(n\)이 커질 때 정규분포에 근접 |
Sample Mean
IID 추출로 크기 \(n\)의 표본 \(Y_1, \dotsc, Y_n\)을 얻었다고 하자. \(Y_i\)가 모평균 \(\mu\)와 모 표준편차 \(\sigma\)를 따른다. 표본 평균의 정의는 다음과 같다.
\[ \ES{Y}_n = \sum_{i=1}^n Y_i. \]
표본 평균과 달리 \(Y_i\)의 기댓값, 즉 모평균은 \(\E (Y_i) \equiv \mu\)라고 쓴다. 여기는 \(n\)이 붙지 않는다. 이는 모평균의 특성으로 일종의 고정된 (미지의) 값이다. 기댓값 \(\E(Y_i)\)를 추정하는 값으로서 표본 평균 \(\ES{Y}_n\)의 세 가지 특징을 알아보자.
- \(\E(\ES Y_n) = \mu\)
- \(\V(\ES Y_n) = {\sigma^2}/{n}\)
Unbiasedness
1에서 보듯이 \(\ES{Y}_n\)은 불편 추정량이다.
Consistency
\(n\)이 증가하면 LLN에 따라서 \(\ES{Y}_n \overset{P}{\longrightarrow} \mu\)가 성립한다.
\(\overset{P}{\longrightarrow}\)는 확률적인 수렴, 즉 앞서 정의를 살펴본 probability limit을 뜻한다. LLN은 약한 버전과 강한 버전이 있다. Kolmogorov의 강한 버전은 증명이 복잡하다. 약한 버전의 증명은 여기를 참고하자. Chebyshev 부등식과 \(\lim_{n \to \infty} \V(\ES{Y}_n) = 0\)을 활용한다.
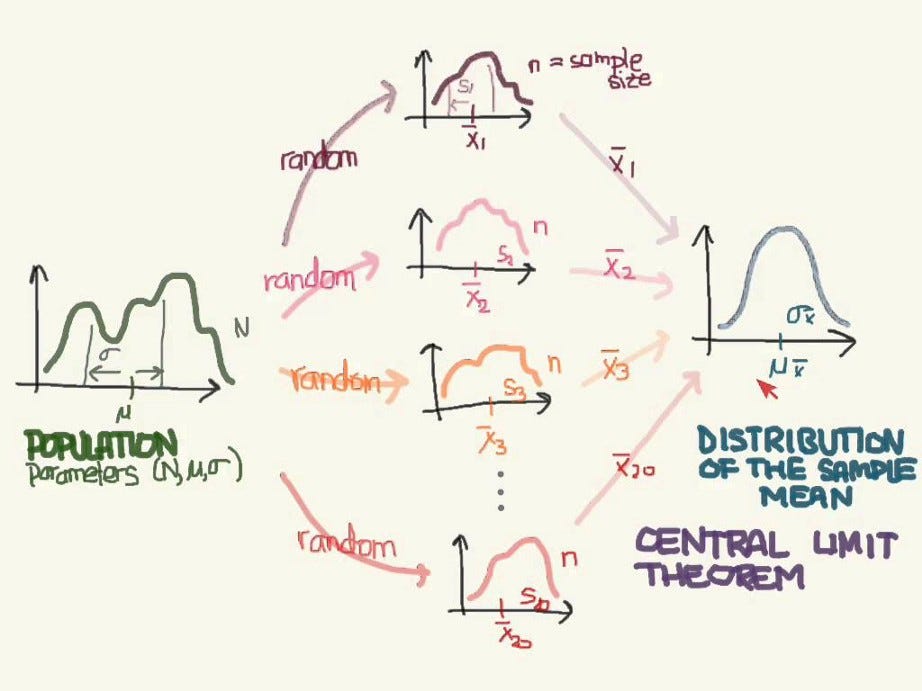
Central Limit Theorem
\[ Z_n = \lim_{n \to \infty} \dfrac{\ES{Y}_n - \mu}{\frac{\sigma}{\sqrt{n}}} \sim \rm N(0,1) \]
Sample Variance
\(\sigma\)의 추정량인 표본 분산 \(S_n\)는 다음과 같다.
\[ S^2_n = \dfrac{1}{n-1} \sum_{i=1}^{n} (Y_i - \ES{Y}_n)^2 \]
\(S^2_n\)은 불편 추정량이고 일치 추정량이다. \(n\)이 충분히 크다면 불편 추정량 여부는 중요하지 않다. \(\dfrac{1}{10000}\)과 \(\dfrac{1}{9999}\)의 차이가 큰 의미가 있을까? 분모의 \((n-1)\) 대신 \(n\)이 들어간 표본 추정량 역시 일치성을 지니고 있다.
Standard Error(SE)
어떤 통계량의 표준 오차(Standard Error)는 표본 통계량의 표준 편차를 뜻한다. 표본 통계량 \(\ES{Y}_n\)의 표준 편차 \(\sqrt{\V(\ES{Y}_n)}\)을 의미한다. \(\sigma^2 < \infty\)를 가정할 때,
\[ \E(\ES{Y}_n - \mu)^2 = \E (\dfrac{\sum(Y_i -\mu)}{n})^2 = \dfrac{1}{n^2} n \sigma^2 = \dfrac{\sigma^2}{n} \]
표준오차 SE는 다음과 같다.
\[ SE = \dfrac{\sigma}{\sqrt{n}} \]
\(SE\)의 추정량 \(\widehat{SE}\)는 \(\sigma\) 대신 \(S_n\)을 사용한다.
\[ \widehat{SE} = \dfrac{S_n}{\sqrt{n}} \]
Asymptotically Normal!
가설 검정에 활용하는 \(t-\)통계량이 정규 분포에 근사하는 이유는 무엇일까?
\[ t(\mu) = \frac{\overline{Y}-\mu}{\widehat{SE}(\overline{Y})} \]
\(t-\)통계량의 분자와 분모를 살펴보면 각각 \(n\)이 커질 때 분자와 분모는 모두 0으로 수렴한다. 이 비율이 정규분포에 수렴한다는 사실은 중심극한 정리를 이용해 증명할 수 있다. 일단 결론만 기억하도록 하자. 요컨대 \(t\)-통계량은 표본 크기 \(n\)이 증가하면서 표준 정규 분포에 근사하게 된다. 다시 말하면 추정량 \(\ES{Y}_n\)은 평균이 \(\mu\)이고 표준편차가 \(\frac{\sigma}{\sqrt{n}}\)인 정규 분포에 근사하게 된다.
\(t-\)통계량은 대 표본(large sample)의 통계적 검정에 기둥이다. 원래 자료가 어느 분포에서 나왔는지와 관계없이 표본 통계량을 활용하는 \(t-\)통계량은 정규 분포를 따르게 되고 이를 통해 가설 검정을 실시할 수 있다.
회귀 분석의 검정 또한 \(t-\)통계량에 근거한다. 여기를 참고하도록 하자.
\(t\)-값은 해당 통계량의 ‘통계적인’ 증거일 뿐이다
\(t-\)통계량의 크기는 검정을 위한 통계학적 증거일 뿐이다. 이 점을 잊지 말자. \(t-\)통계량의 형태에서 보듯이 분자가 충분히 크거나 혹은 분모가 충분히 작을 때 이 값이 커진다. 이는 신뢰 구간에 대해서도 마찬가지다. 신뢰 구간은 표준 오차에 반영되어 있는 통계적 정밀성에 의해 결정되지 우리가 발견하고자 하는 관계의 내용상 강도에 의해서 결정되지 않는다. 즉 \(t-\)통계량 및 신뢰 구간의 모습을 보고 해당 독립 변수가 종속 변수에 미치는 효과의 강도로 오해하면 곤란하다.
울드리지 교수는 이를 통계적 유의성과 실용적 유의성의 차이로 설명한다. 통계적으로 유의미한 변수를 찾으면 우리는 대체로 기분이 좋아진다. 하지만 통계적으로 유의한 그 관계가 실용적으로도 그럴까? 만일 통계적 유의성을 지닌 계수가 사실상 의미가 없는 경우라면 어떨까? 책을 읽을 때 다리를 떨면 책을 읽는 속도가 통계적으로 유의미하게 0.1% 증가한다고 하자. 이는 사실상 의미 있는 결과일까? (책을 읽을 때는 열심히 다리를 떨어라?)
More
이하의 내용은 딱히 필요하지는 않다. 관심이 있는 경우는 살펴보면 좋겠다.
\(S^2\)을 \((n-1)\)로 나누는 이유
\(S^2\)의 분모에 왜 \((n-1)\)이 들어갈까? 불편 추정량을 얻기 위해서다. 불편 추정량이란 해당 통계치의 기댓값이 모수가 되는 추정량을 의미한다. 직접 \(S^2\)의 기댓값을 구해보자. 먼저,
\[ \begin{aligned} \sigma^2 = {\rm Var}(x_i) & = \mathbb E[(x_i - \mu)^2] \\ & = \mathbb E [x_i^2 - 2 x_i \mu + \mu^2] \\ & = \mathbb E(x_i^2) - 2\mu E(x_i) + \mu^2 \\ & = \mathbb E(x_i^2) - \mu^2 \end{aligned} \]
\(\mathbb E(x_i^2) = \sigma^2 + \mu^2\) 임을 기억해두자.
이제 \(S^2\)의 기댓값을 구해보자. 분자 먼저 계산하자.
\[ \begin{aligned} \mathbb E[\sum(x_i - \overline{x})^2] & = \mathbb E[\sum (x_i^2 - 2 x_i \overline{x} + \overline{x}^2)] \\ & = \mathbb E[\sum x_i^2 - n 2 \overline{x} \cdot \overline{x} + n \overline{x}^2] \\ & = \mathbb E[\sum x_i^2 - n \overline{x}^2)] \\ & = \sum \mathbb E(x_i^2) - n \mathbb E(\overline{x}^2) \end{aligned} \]
합해지는 부분의 각각을 따져보자.
\[ \begin{aligned} \sum \mathbb E(x_i^2) = n (\sigma^2 + \mu^2) \end{aligned} \]
\[ \begin{aligned} \mathbb E(\overline{x}^2) & = \mathbb E[(\dfrac{x_1 + x_2 + \dotsb + x_n}{n})^2] \\ \end{aligned} \]
- \(\mathbb E[(\dfrac{x_1 + x_2 + \dotsb + x_n}{n})^2]\)의 분자를 계산하면 된다. 먼저 각 \(x_i\)의 제곱이 \(n\)개 나온다. 다음으로 각각 \(x_i\)가 독립적으로 추출되었으므로 \(i \neq j\)일 때 \(\mathbb E(x_i x_j) = \mathbb E(x_i) \mathbb E(x_j) = \mu^2\)이 된다. \(n\) 개 중에서 2개를 순서에 관계없이 뽑게 된다. 즉,
\[ \begin{aligned} \mathbb E[(x_1 + x_2 + \dotsb + x_n)^2] & = n (\sigma^2 + \mu^2) + 2 \dfrac{n(n-1)}{2!} \mu^2 \\ & = n \sigma^2 + n^2 \mu^2 \end{aligned} \]
따라서,
\[ \mathbb E(\overline{x}^2) = \dfrac{\sigma^2}{n} + \mu^2 \]
이제 각각을 넣어 계산을 완료하자.
\[ \begin{aligned} \mathbb E[\sum(x_i - \overline{x})^2] & = \sum \mathbb E(x_i^2) - n \mathbb E(\overline{x}^2) \\ & = n \sigma^2 + n \mu^2 - \sigma^2 - n \mu^2 \\ & = (n-1) \sigma^2 \end{aligned} \]
따라서 불편 추정량이 되기 위해서는 \(S^2\)의 분모에 \((n-1)\)이 필요하다.
\(S^2_n\)의 일치성
\(S^2\)의 일치성을 증명하는 데 필요한 내용을 알아보자. 엄밀한 증명은 생략하고 간략하게 아이디어만 적도록 하겠다. \(\sigma < \infty\)를 가정하자. 이때
\[ \begin{aligned} S_n^2 & = \dfrac{1}{n-1}\sum_{i=1}^n (X_i - \overline{X}_n) \\ & = \dfrac{n}{n-1}(\dfrac{\sum X_i^2}{n} - \overline X_n) \\ & \stackrel{P}{\longrightarrow} 1\cdot(\E(X^2)-\mu^2) = \sigma^2 \end{aligned} \]
위에서 보듯이 \(S^2_n\)이든 \(\dfrac{1}{n}\sum_{i=1}^n (X_i - \overline{X}_n)\)이든 둘 다 일치 추정량이라는 것을 쉽게 알 수 있다.
자세한 내용은 여기 책의 해당 부분을 참고하라.
회귀 분석의 \(t-\)통계량
회귀 분석의 계수의 표본 추정량 \(\hat \beta\)는 다음과 같다. \[ \hat \beta = (X^T X)^{-1}(X y) \]
\[ t_i = \dfrac{\hat \beta_i - \beta}{S \sqrt{(X^T X)_{ii}^{-1}}} \]
with
\[ S(y_i)^2 = \dfrac{1}{n-k} \sum_{i=1}^n (y_i - x^r_i \hat\beta) \]
여기서 \(\beta_k\)는 중회귀 분석의 \(k\)–번째 계수를 뜻한다.
- \(x^r_i\): \(X\)의 \(i\)’th 행(row) 벡터
- \(\underset{(1 \times k)}{x^r_i}\underset{(k \times 1)}{\vphantom{x^r_i}\hat\beta} = \hat y_i\)
회귀 분석의 \(i\)–번째 계수인 \(\beta_i\)는 \(t_i\)를 통해 검정할 수 있다. \(n\)이 충분히 클 경우 \(t_i \sim \rm N(0,1)\)이 된다.
CLT and LLN illustrated
LLN과 CLT은 동전의 양면처럼 보이기도 한다. 아래 첫번째 그림에서 보듯이 \([0,1]\) 사이를 고정해서 보면 표본의 크기가 증가할수록 분산이 줄어들게 되고 추정량이 파라미터 주변으로 모이게 된다. 반면, 두번째 그림에서 보듯이, 표본의 크기에 따라서 \(x\) 축의 비율을 조절하면 분포가 점점 정규 분포를 닮아간다.