# Basic packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
# Stats models
import statsmodels.formula.api as sm
import statsmodels.stats.sandwich_covariance as sw
import statsmodels as statsmodels
def generate_unit_df(pack_of_cigar, n, sd=1, covid_threshold=2, cigar_threshold=6):
mean_of_severity_covid = pack_of_cigar * 0.3
mean_of_severity_cigar = pack_of_cigar * 1.4
df = pd.DataFrame(
{
'pack_of_cigar': pack_of_cigar,
'covid_severity': np.random.normal(mean_of_severity_covid, 1, n),
'cigar_severity': np.random.normal(mean_of_severity_cigar, 0.5, n)
}
)
df = df.assign(
**{
'covid_severity': np.where(df['covid_severity'] > 0, df['covid_severity'], 0),
'cigar_severity': np.where(df['cigar_severity'] > 0, df['cigar_severity'], 0),
'is_hospitalized': np.where((df['covid_severity'] > covid_threshold) | (df['cigar_severity'] > cigar_threshold), "Yes", "No"),
'is_observed': np.random.uniform(0, 1, n)
}
)
df = df.query(
"(`covid_severity` <= 3.5)"
)
df = df.query(
"(`is_hospitalized` == 'Yes') | (`is_hospitalized` == 'No' & `is_observed` <= 0.2)"
)
df = df.query(
"(`is_hospitalized` == 'No' & `is_observed` <= 0.2) | (is_observed <= 0.5)"
)
return df
res = pd.DataFrame()
for pack in np.linspace(0, 6, 60):
n = int(np.random.uniform(20, 40, 1)[0])
res = pd.concat([res, generate_unit_df(pack,n)])Berkson’s Paradox with Regression
회귀 분석으로 보는 벅슨의 역설
심슨의 역설과 마찬가지로 벅슨의 역설을 보통 회귀 분석으로 설명하지 않는다. 그런데 이 문제 역시 회귀 분석으로 보면 보다 명확해진다. 벅슨의 역설은 인과 추론에서 말하는 충돌 요인(collider)의 맥락에서 주로 발생한다. 정확히 말하면 벅슨의 역설은 변인의 통제 여부보다는 (인지하지 못하는) 표본의 제한성에서 비롯한다. 아쉽게도 벅슨의 역설을 예시하는 현실 데이터는 별로 없다. 여기서는 충돌 요인을 일으키는 플롯을 상정하고 이에 맞춰 가상의 데이터를 생성한다. 회귀 분석을 통해 이 데이터를 다시 음미하면서 벅슨의 역설을 살펴보도록 하자.
플롯
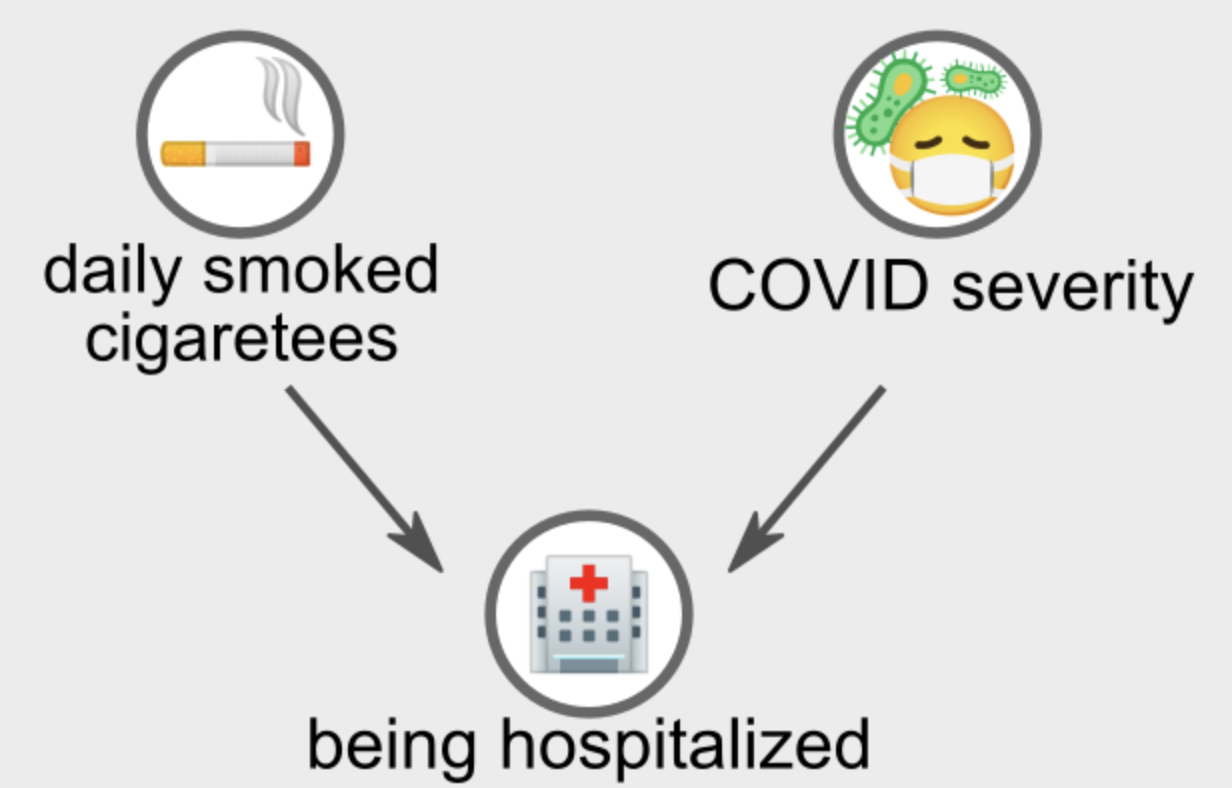
여기 적는 내용은 스토리텔링이지만 또 단순한 스토리텔링은 아니다. 코로나19와 흡연의 관계를 조사하기로 한 연구자가 있다고 하자. 그는 입원 환자의 자료를 살펴보고 놀라운 결론을 얻었다. 흡연하는 사람일수록 코로나 증세가 덜 심하다는 관계를 파악했다. 일반적인 통념과 반대되는 결론을 얻었던 것이다. 이것이 맞는 분석일까? 먼저 아래의 인과 다이어그램을 보자.
이 연구는 코로나19 인식에 있어서 충돌 요인의 문제를 다양하게 지적하고 있다.
담배를 많이 피울수록 혹은 그래왔을수록 코로나19 이외의 요인으로도 병원에 입원할 가능성이 높아진다. 또한 코로나 증세가 심할수록 병원에 입원할 가능성이 높아진다. 이 경우 병원에 입원한다는 변인이 두 요인(흡연의 정도, 코로나19 중증도) 모두에 영향을 받는 충돌 요인이 된다. 따라서 충돌 요인을 통제할 경우 흡연의 정도와 코로나19의 중증도 사이의 관계가 왜곡된다. 이러한 취지로 데이터를 생성해보도록 하자.
위의 플롯에 따라서 가상의 데이터를 생성했다. 코로나19 중증도는 흡연의 정도에 양의 영향을 받는다. 그리고 흡연의 정도는 별도로 건강에 악영향을 준다. 따라서 코로나19 중증도, 흡연의 정도 모두 해당 환자가 입원할 가능성을 결정하게 된다.
palette = sns.color_palette("dark")
#sns.palplot(palette)
plt.rcParams['figure.figsize'] = [8, 4]
plt.style.use("fivethirtyeight")# for pretty graphs
sns.set(font_scale=0.7)
fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True)
sns.regplot(x = 'pack_of_cigar',y = 'covid_severity', data = res, ax=ax1, color='grey',scatter_kws={'alpha': 0.4})
#
for i, value in enumerate(res['is_hospitalized'].unique()):
ax2 = sns.regplot(x="pack_of_cigar", y="covid_severity",
#color=colors[value],
#marker=markers[i],
scatter_kws={'alpha': 0.3 if value == "Yes" else 0.15},
data=res[res['is_hospitalized'] == value],
label=value,
ax = ax2)
ax2.legend(loc='best')
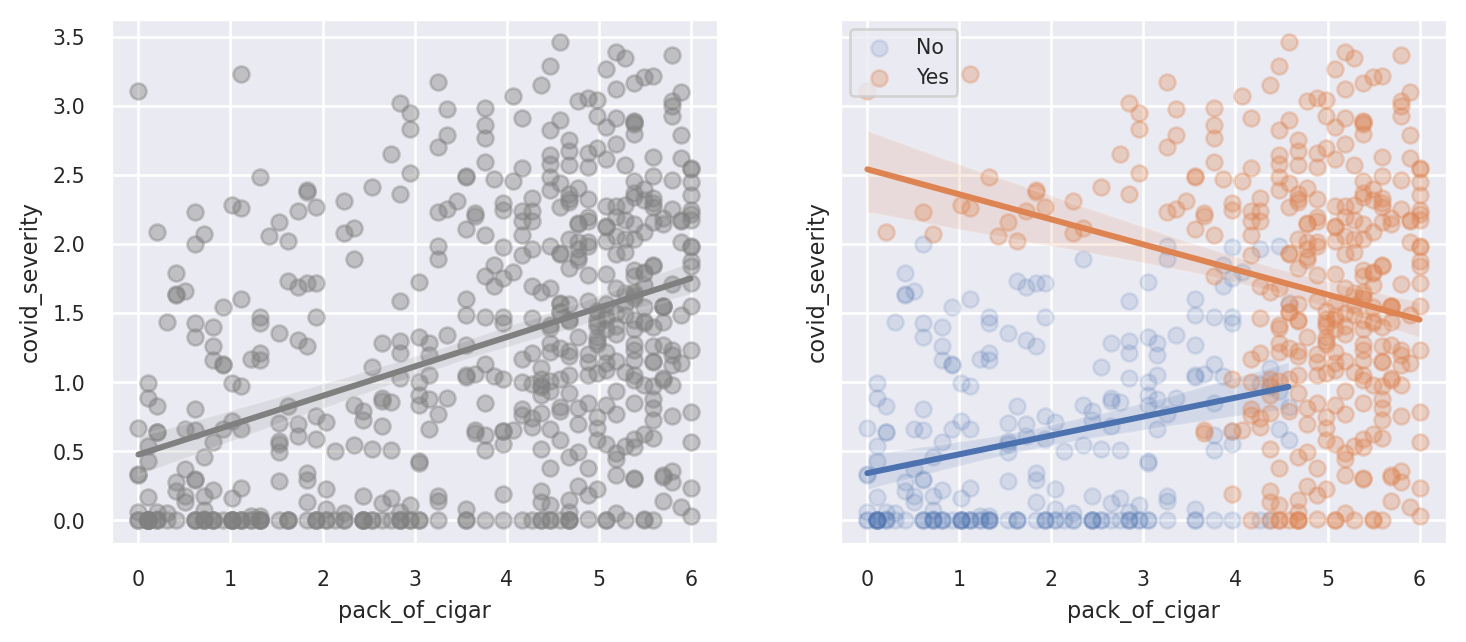
ax1.set_aspect(1.5); ax2.set_aspect(1.5)위의 왼쪽 그래프에서 보듯이 추출된 표본 전체에 대해서는 흡연의 정도와 코로나19의 중증도 사이에 양의 관계가 존재한다. 그런데 만일 충돌 요인인 입원 여부를 회귀 분석에서 통제하면 어떻게 될까? 오른쪽 그림에서 보듯이 병원에 입원한 환자에 대해서는 음의 상관성이 관찰된다. 왜 이럴까? 병원의 입원하는 변인은 코로나19의 중증도 이외에 흡연 정도에도 영향을 받는다. 흡연을 많이 할수록 코로나와 관계없이 그 자체로 입원할 가능성이 커진다. 흡연 정도가 낮을 경우 입원을 했다면 코로나19의 중증도에 따른 것일 가능성이 크다. 반면 흡연 정도가 높을 경우 코로나19 중증도는 상대적으로 다양한 상태를 지니게 되고, 따라서 평균적으로는 흡연 정도가 낮은 입원 환자에 비해서 낮은 코로나19 중증도를 지닐 수 있다.
ols1 = sm.ols(formula="covid_severity ~ pack_of_cigar", data=res).fit(use_t=True)
ols2 = sm.ols(formula="covid_severity ~ pack_of_cigar + is_hospitalized", data=res).fit(use_t=True)
ols3 = sm.ols(formula="covid_severity ~ pack_of_cigar + is_hospitalized", data=res[res.is_hospitalized=="Yes"]).fit(use_t=True)
#ols1.summary()
#ols2.summary()
#stargazer sucks
from stargazer.stargazer import Stargazer
stargazer = Stargazer([ols1, ols2, ols3])
stargazer
#regs = [ols1, ols2, ols3]
#from statsmodels.iolib.summary2 import summary_col
#print(summary_col(
# regs,
# stars=True,
# float_format='%0.2f',
# model_names=['(1)','(2)','(3)'],
# info_dict={
# 'N':lambda x: "{0:d}".format(int(x.nobs)),
# 'F': lambda x: "{0:.2f}".format(x.fvalue),
# },
# regressor_order=['Intercept','pack_of_cigar','is_hospitalized[T.Yes]#'])
# )
| Dependent variable: covid_severity | |||
| (1) | (2) | (3) | |
| Intercept | 0.474*** | 0.646*** | 2.540*** |
| (0.081) | (0.076) | (0.215) | |
| is_hospitalized[T.Yes] | 1.133*** | ||
| (0.105) | |||
| pack_of_cigar | 0.213*** | -0.022 | -0.182*** |
| (0.020) | (0.028) | (0.044) | |
| Observations | 572 | 572 | 341 |
| R2 | 0.164 | 0.307 | 0.047 |
| Adjusted R2 | 0.163 | 0.305 | 0.045 |
| Residual Std. Error | 0.870 (df=570) | 0.793 (df=569) | 0.873 (df=339) |
| F Statistic | 112.101*** (df=1; 570) | 126.278*** (df=2; 569) | 16.876*** (df=1; 339) |
| Note: | *p<0.1; **p<0.05; ***p<0.01 | ||
회귀 분석에서 이러한 결과를 잘 확인할 수 있다. 회귀 분석에서 현실에 가장 근접한 분석은 회귀식 (1)이다. 입원 여부를 통제하게 될 경우(회귀식 (2))는 흡연의 정도가 코로나19의 중증도에 미치는 영향을 왜곡하게 된다. 벅슨의 역설의 극단적인 버전은 입원한 환자만 표본으로 삼아 분석을 실시하는 경우이다. 회귀식 (3)에서 보듯이 흡연의 정도와 코로나19 중증도의 정도가 가장 많이 왜곡된다.
\(\mathrm R^2\) 값을 무조건 분석의 성과 지표로 삼으면 안 되는 이유도 확인하고 지나가자. 충돌 요인 변수가 통제되면 \(\mathrm R^2\)은 증가한다. 설명 변수가 늘어날수록 설명 변수의 차원이 높아지게 되므로 벡터 공간에서 잔차의 길이가 줄어들게 된다. 이는 동어 반복에 가깝다. 위에서 보듯이 \(\mathrm R^2\)가 줄었으니 분석력이 더 높아진 것일까?
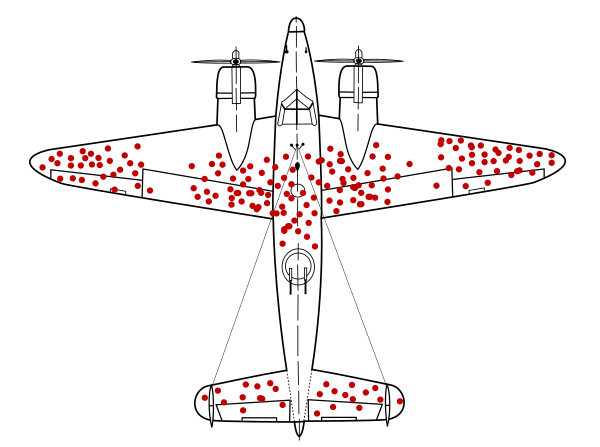
벅슨의 역설은 생존자 편향(survivorship bias)과도 일맥상통한다. 유명한 아래의 그림을 다시 확인해보자. 살아 돌아온 비행기들이 맞은 부위는 오히려 보강이 필요하지 않은 부위다. 돌아오지 못한 비행기들은 현재 생존한 비행기들이 맞지 않은 부위 때문에 추락했을지 모른다.