Simpson’s Paradox with Regression

regression

stats-simple

펭귄의 부리로 직접 계산해보자.

Author

JS HUHH

Published

June 5, 2022

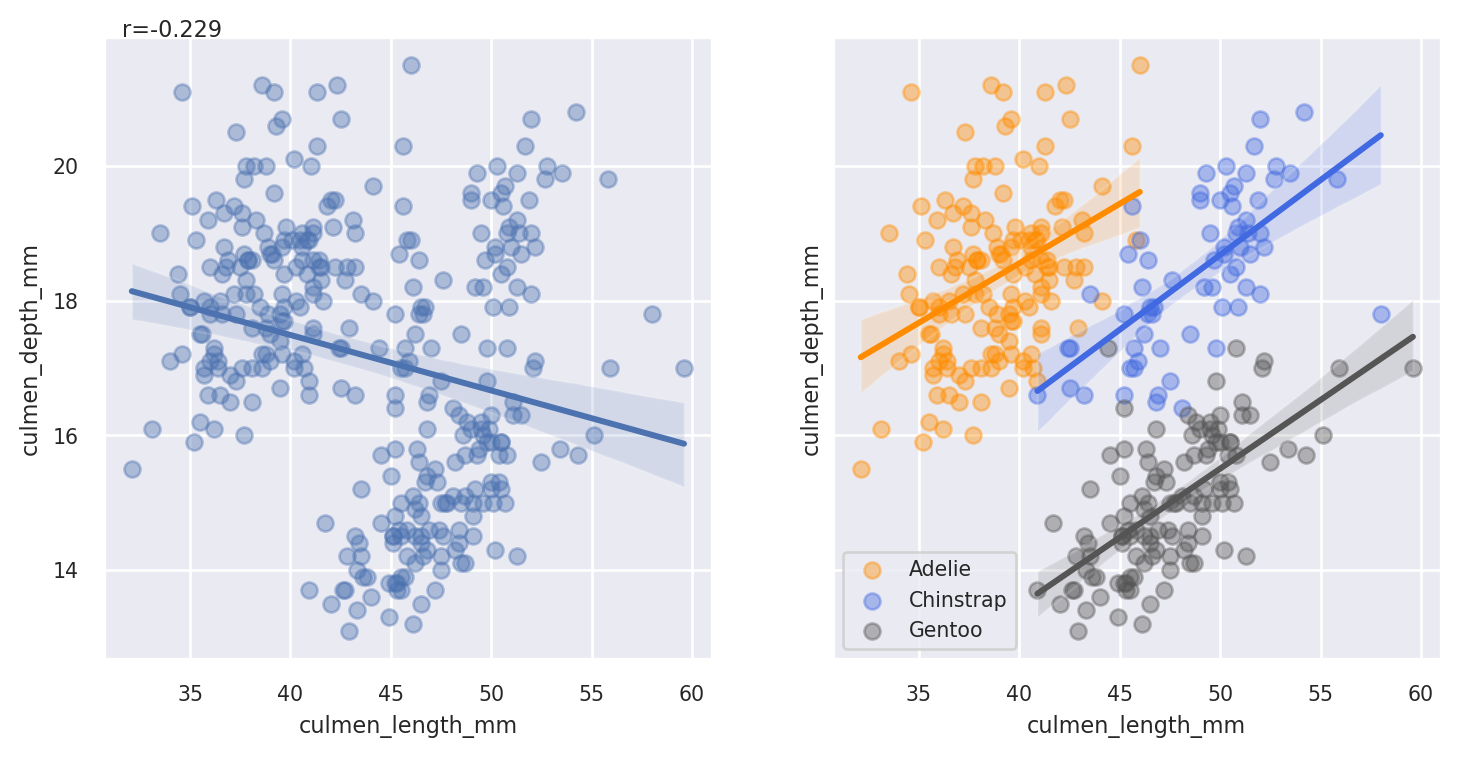
회귀 분석으로 보는 심슨의 역설

심슨의 역설을 보통은 회귀 분석으로 설명하지 않는다. 그런데 회귀 분석으로 보면 보다 명확하다. 심슨 역설의 전형적인 사례를 펭귄 부리의 길이와 높이를 통해 살펴보도록 하자.

데이터는 여기를 참고하자.

culmen은 새의 부리를 뜻한다. 옆 그림에서 보듯이 length는 부리의 앞으로 튀어나온 길이를, depth는 부리의 높이를 의미한다. 아래 보듯이 이 데이터는 펭귄의 세 가지 종족, 성별 등을 별도로 담고 있다.

 # Basic packages
import pandas as pd 
import numpy as np
import pandas as pd
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as plt
# Stats models pip 
import statsmodels.formula.api as sm
import statsmodels as statsmodels
%matplotlib inline

csv_addr = "data/penguins_size.csv"
plt.style.use("fivethirtyeight")# for pretty graphs
df  = pd.read_csv('data/penguins_size.csv')
df.head();
#df.info();
df = df.dropna()
df.info()

<class 'pandas.core.frame.DataFrame'>
Index: 334 entries, 0 to 343
Data columns (total 7 columns):
 #   Column             Non-Null Count  Dtype  
---  ------             --------------  -----  
 0   species            334 non-null    object 
 1   island             334 non-null    object 
 2   culmen_length_mm   334 non-null    float64
 3   culmen_depth_mm    334 non-null    float64
 4   flipper_length_mm  334 non-null    float64
 5   body_mass_g        334 non-null    float64
 6   sex                334 non-null    object 
dtypes: float64(4), object(3)
memory usage: 20.9+ KB

plt.rcParams['figure.figsize'] = [8, 4]
sns.set(font_scale=0.7)

fig, (ax1, ax2) = plt.subplots(ncols=2, sharey=True)
sns.regplot(x = 'culmen_length_mm',y = 'culmen_depth_mm', data = df, scatter_kws={'alpha': 0.4}, ax=ax1)
r = stats.pearsonr(df['culmen_length_mm'], df['culmen_depth_mm'])[0]
ax1.text(.03, 1, 'r={:.3f}'.format(r), transform=ax1.transAxes)
colors = ['darkorange', 'royalblue', '#555555']
markers = ['.', '+', 'x']
#
for i, value in enumerate(df['species'].unique()):
    ax2 = sns.regplot(x="culmen_length_mm", y="culmen_depth_mm", ax=ax2,
                      scatter_kws={'alpha': 0.4},
                     color=colors[i],
                     #marker=markers[i],                      
                     data=df[df['species'] == value],
                     label=value)
ax2.legend(loc='best');

패널의 왼쪽 그림에서 보듯이 종 구분 없이 펭귄 부리의 길이와 높이를 보면 서로 음의 상관성을 지니고 있는 듯 보인다. 그런데 이를 종별로 구별해서 살펴보면 오히려 길이와 높이는 양의 상관성을 지니고 있다.

ols1 = sm.ols(formula="culmen_depth_mm ~ culmen_length_mm", data=df).fit(use_t=True)
ols2 = sm.ols(formula="culmen_depth_mm ~ species + culmen_length_mm", data=df).fit(use_t=True)
ols3 = sm.ols(formula="culmen_depth_mm ~ species * culmen_length_mm", data=df).fit(use_t=True)
#ols1.summary()
#ols2.summary()

from stargazer.stargazer import Stargazer
stargazer = Stargazer([ols1, ols2, ols3])
stargazer

#regs = [ols1, ols2, ols3]
#from statsmodels.iolib.summary2 import summary_col
#print(summary_col(
#                  regs,
#                  stars=True, 
#                  float_format='%0.2f',
#                  model_names=['(1)','(2)','(3)'],
#                  info_dict={
#                    'N':lambda x: "{0:d}".format(int(x.nobs)), 
#                    'F': lambda x: "{0:.2f}".format(x.fvalue),
#                    }, 
#                  regressor_order=['Intercept','culmen_length_mm','secies'])
#    )


	Dependent variable: culmen_depth_mm

	(1)	(2)	(3)

Intercept	20.786^***	10.619^***	11.488^***
	(0.854)	(0.691)	(1.162)
culmen_length_mm	-0.082^***	0.199^***	0.177^***
	(0.019)	(0.018)	(0.030)
species[T.Chinstrap]		-1.919^***	-3.919^*
		(0.226)	(2.070)
species[T.Chinstrap]:culmen_length_mm			0.046
			(0.046)
species[T.Gentoo]		-5.080^***	-6.187^***
		(0.194)	(1.778)
species[T.Gentoo]:culmen_length_mm			0.027
			(0.041)

Observations	334	334	334
R²	0.052	0.766	0.767
Adjusted R²	0.049	0.764	0.764
Residual Std. Error	1.919 (df=332)	0.956 (df=330)	0.957 (df=328)
F Statistic	18.313^*** (df=1; 332)	360.759^*** (df=3; 330)	216.026^*** (df=5; 328)

Note:	^p<0.1; ^p<0.05; ^**p<0.01

회귀 분석에서 종을 통제한 경우와 그렇지 않은 경우의 culmen_length_mm(부리의 길이)의 계수를 비교해보자. (1)은 종족을 통제하지 않은 회귀식으로 culmen_length_mm의 계수는 음수이다. 반면 종족을 통제한 (2)의 회귀식은 종족의 구분해 각 절편과 해당 종족 내의 부리의 길이와 높이의 관계를 계산해 이를 적절하게 가중 평균한 값이 culmen_length_mm의 계수가 된다. 회귀 테이블에서 보듯이 culmen_length_mm의 계수는 음수에서 양수로 바뀌어 있다.

나머지 계수의 의미는 기본이 되는 Adelie 종족을 기준으로 다른 두 개의 종족의 절편이 얼마나 떨어져 있는지를 보여준다. 회귀식을 적어보면 다음과 같다.

식 (1) \(y_i = \alpha_i + \beta x_i\)

식 (2) \(y_i = \alpha_i + \beta x_i + D_{1i} + D_{2i}\)

\(y_i\): culmen_depth_mm 부리의 높이
\(x_i\): culmen_length_mm 부리의 길이
\(D_{1i}\): 종족이 Chinstrap일 경우 1 이외는 0
\(D_{2i}\): 종족이 Gentoo일 경우 1이외는 0

식 (3)은 \(\beta_i\)가 그룹별로 달라지는지 여부를 교호작용 항목을 통해 확인했다. (3)이 보여주듯이 그룹별로 \(\beta_i\)는 통계적으로 유의미한 차이가 없다.