정규성에 집착하지 말자.
TL; DR
- 샘플 크기가 충분하다면 가설 검정 시 정규 분포 가정에 집착할 필요가 없다!
- 가설 검정에서 중요한 것은 ’표본 (통계량)’의 분포이지 ’모집단’의 분포가 아니다!
정규 분포는 필요한 가정인가?
표분의 크기가 크지 않다면 가설 검정을 위해 (정규) 분포 가정이 필요하다. 하지만 표본의 크기가 어느 정도 이상일 때도 가설 검정을 위해 정규 분포 가정이 필요할까? 아래와 같은 다중 회귀 분석 모형을 보자.
\[ Y_i = \alpha + \beta_1 X_{1i} + \beta_2 X_{2i} + \dotsb + \beta_n X_{ni} + \epsilon_i \]
원래 정규 분포 가정은 \(\epsilon_i \sim \rm N (0, \sigma^2)\)이다. 그런데 우리는 이 가정을 어떻게 확인할 수 있을까?
\(Y_i \sim \rm N(\cdot)\)을 확인하면 될까? 원래의 가정은 오차항에 대한 가정이다. 앞에 여러 가지 변수의 작용으로 \(Y_i\)가 결정되므로 \(Y_i\)가 정규 분포를 따르는 것이 \(\epsilon_i\)가 정규분포를 따르는 것의 충분 조건이 되지 않는다. 반면 \(\epsilon_i\)가 정규 분포를 따른다고 해서 반드시 \(Y_i\)가 정규 분포를 따른다고 볼 수도 없다.
\(\hat\epsilon_i = Y_i - \hat{Y}_i\)가 정규 분포를 따르면 될까? 이 역시 \(\hat\epsilon_i\)이 정규 분포를 따른다고 해서 \(\epsilon_i\)가 정규 분포를 따르리라고 볼 수 없다. \(\hat\epsilon_i\)는 회귀 분석의 모델링 아래 도출된 \(\epsilon_i\)에 관한 추정치일 뿐이다. 추정치가 정규 분포를 따르는 것이 모수가 정규 분포를 따르는 것의 충분 조건이 되지는 않는다.
회귀 분석에서 오차항은 모델링을 위한 일종의 ’가정’이다. 모델링의 가정은 받아들이는 것이지 검증하는 것이 아니다.
표본이 크지 않을 때 즉 소 표본에 적합한 분석 방법을 찾는 것은 대 표본의 경우에 비해 까다로운 문제이다. 그런데 소 표본에서 회귀 분석은 그리 나쁜 분석 방법이 아니다.
표본의 크기가 충분히 크다면…
만일 가정을 받아들일 수 없다면 회귀분석에서 가설 검정을 수행할 수 없을까? 그렇지 않다는 점을 우리는 이미 잘 알고 있다. 만일 표본의 크기가 충분히 크다면 오차 항의 정규 분포 가정 없이도 중심 극한 정리를 활용해 가설 검정을 할 수 있다.
행렬을 활용해 나타낸 회귀 분석의 계수의 표본 추정량 \(\hat \beta\)는 다음과 같다. \[ \hat \beta = (X^T X)^{-1}(X y) \]
회귀 분석에서 \(\beta_i\)를 검정하기 위한 \(t\)-통계량은 다음과 같이 정의된다.
\[ t_i = \dfrac{\hat \beta_i - \beta}{S \sqrt{(X^T X)_{ii}^{-1}}} \]
with
\[ S(y_i) = \sqrt{\dfrac{1}{n-k} \sum_{i=1}^n (y_i - \hat y_i)^2} \]
여기서 \(\hat y_i = \underset{(1 \times k)}{x^r_i}\underset{(k \times 1)}{\vphantom{x^r_i}\hat\beta}\)이고, \(x^r_i\)은 \(X\)의 \(i\)’th 행(row) 벡터를 나타낸다.
\(n\)이 커짐에 따라서 \(t_i\)의 분포는 \(\rm N(0,1)\)에 점점 다가간다. ’중심극한 정리’가 가설 검정에서 중요한 이유가 여기에 있다.
\(\sqrt{n}(\beta_i - \beta) \overset{d}{\longrightarrow} \rm N (0, \sigma_i)\) 직관적으로 설명하면 \(t_i\)의 분자와 분모 모두 0으로 수렴한다. 이때 분자와 분모의 수렴이 일정한 분포, 정규 분포로 수렴한다는 것이 중심 극한 정리이다.
요약하면 표본의 크기가 충분할 때 오차 항의 정규 분포 가정은 잊어도 좋다. 이 가정이 없어도 중심 극한 정리에 따라서 필요한 가설 검정을 수행할 수 있다. \(t\)-값과 표준 정규 분포에 근거한 개별 계수의 검정 그리고 F–값과 F 분포에 근거한 전체 계수의 검정이 모두 가능하다. \(t\)-값은 항상 \(t\) 분포를 따를까? 대 표본이라면, 대략 \(n \geq 30\), t 분포라고 보든 정규 분포라고 보든 문제가 될 것이 없다. 따라서 대표본에서 굳이 \(t\) 분포를 고집할 필요는 없다. 사실 표본의 수가 어느 정도 이상이면 \(t\) 분포의 값과 정규 분포의 값의 차이는 무시해도 좋을 만큼 작다.
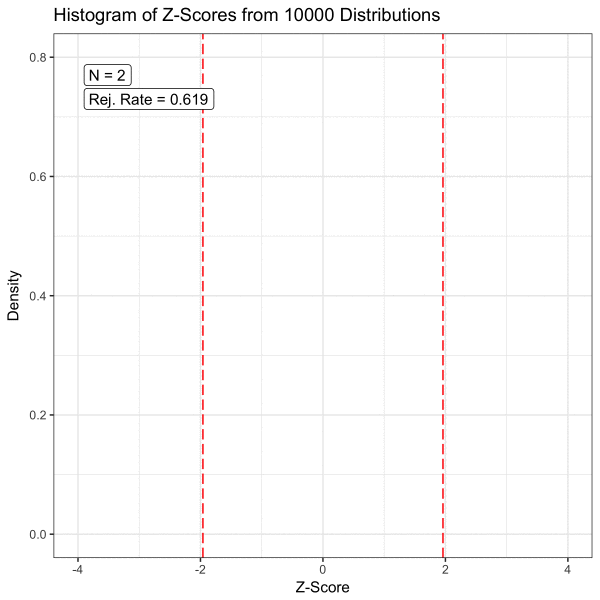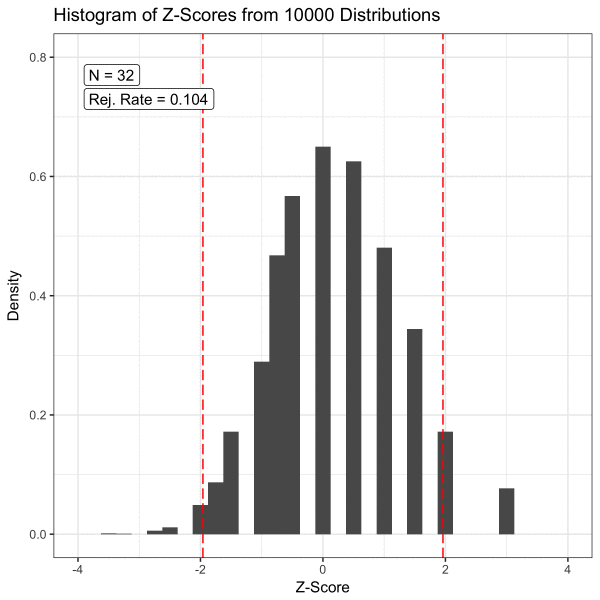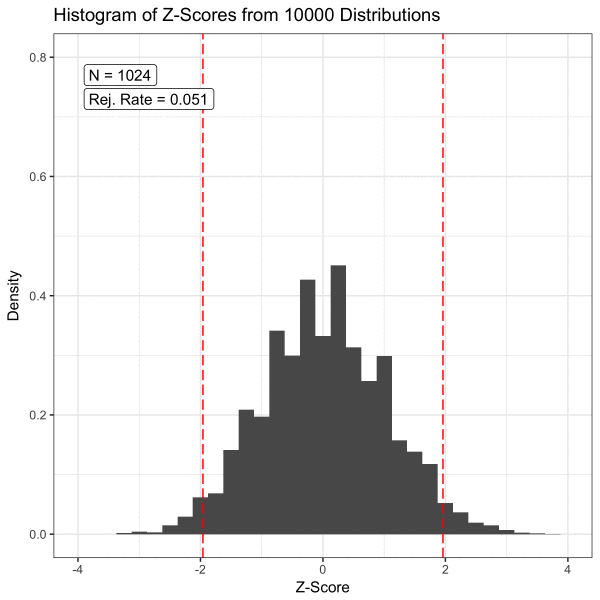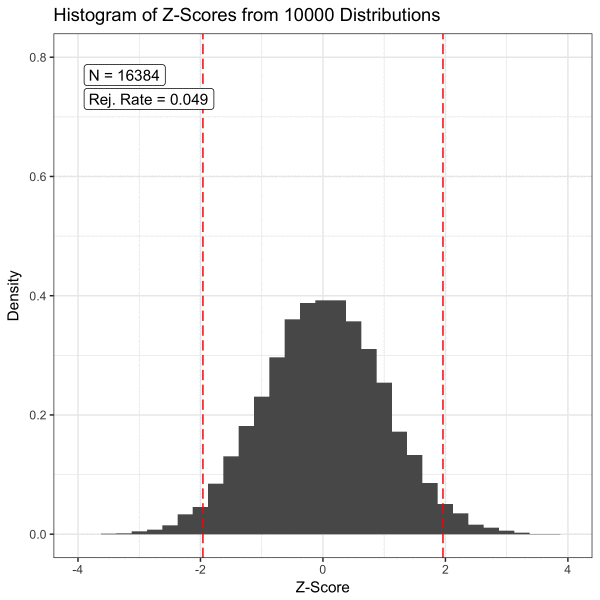
표본의 크기가 얼마나 크면 될까? Schmidt and Finan의 연구에 따르면 회귀 모형의 경우 변수 당 대략 10개 이상의 관찰이 필요하다. 옆 그림에서 보듯이 모평균을 추정하는 문제에서 표본 평균의 크기가 30개 이상이면 CLT을 적용할 수 있다.
위 그림에서 보듯이 가설 검정에서 모집단의 분포는 우리의 관심사가 아니다. 우리의 관심사는 표본 통계량이고, 이 표본 통계량이 얼마나 믿을만 할지를 가설 검정을 통해 파악한다. 후자를 가능하게 하는 것이 대 표본의 표본 통계량에 대해 성립하는 중심 극한 정리인 셈이다.
물론 주의해야 할 점이 있다. 중심 극한 정리를 제대로 쓰기 위해서는 표본 분산 \(S^2\)의 추정이 중요하다. 만일 어떤 이유에서건 분산의 추정에 방해하는 요인이 개입한다면 이에 따라서 가설 검정도 흔들릴 수 밖에 없다. 때문에 정규성보다는 등분산성 그리고 내생성 등에 더 신경을 쓰는 편이 낫다.