조건 명제 그리고 부정
TL; DR
- 조건 명제가 의미하는 것을 확인해보고, 조건 명제의 ’부정’도 도출해보자.
- 함수 극한의 엡실론-델타 정의를 통해 조건 명제의 의미를 연습해보자.
조건 명제
조건 명제는 잘 아는 듯싶지만, 내게는 가끔 혼란의 시간이 찾아오더라. 이 기회에 생각나는 대로 한번 정리해 보겠다. 아울러 극한의 정의까지 응용편으로 살펴보겠다.
용어 정리
- 명제: 참과 거짓을 가릴 수 있는 언술을 의미한다. 배중률(law of excluded middle)에 따르면 명제는 참 혹은 거짓 중 하나만 될 수 있다. 참과 거짓이 동시에 성립하거나 혹은 동시에 성립하지 않거나 할 수 없다.
- 진리 집합(truth set): 진리 집합을 정의하기 위해서는 위에서 설명한 명제 그리고 변수가 필요하다. 변수는 명제에서 변할 수 있는 부분이다. 변수를 주어 그리고 명제의 설명에 해당하는 부분을 술어(predicate)라고 칭하기도 한다. 진리 집합이란 특정 명제를 만족시키는 모든 변수 값들의 집합을 나타낸다.
- 명제: \(x > 3\)
- 변수: \(x\)
- 진리집합: \(\{ x \in \mathbb R | x > 3 \}\)
명제를 진리 집합과 연결해 생각하면 편리할 때가 있다. 명제의 여러 가지 조작을 집합으로 바꿔 생각하면 익숙한 ’벤 다이어그램’을 활용할 수 있다.
조건 명제(conditional proposition)
조건 명제는 “만일 \(p\;\)이면, \(q\;\)가 성립한다”와 같이 표현한다. 동일한 의미를 지니는 표현을 몇 가지 더 알아보자.
- \(p \implies q\)
- If \(p\), then \(q\).
- \(p\) implies \(q\).
- \(p\) is sufficient condition for \(q\).
이 관계는 형식 논리의 관계이지 ‘인과’ 관계가 아니다. 즉, 형식 논리상 명제 \(p\) 와 명제 \(q\) 사이의 관계를 기계적으로 서술한다. 진리 집합으로 보자. \(p\)의 진리집합 \(P\)와 \(q\)의 진리집합 \(Q\)가 있다고 하자. 조건 명제가 참이라면, \(P \subset Q\)이다.
\(p \implies q\)는 진리집합으로 본다면 \(P\)에 속하는 모든 원소는 \(Q\)에 속해야 한다는 뜻이다. 즉, \(p\)라는 명제를 만족하는 모든 경우에 대해서 \(q\)가 만족해야 한다.
진리표
이를 이해하고 나면 \(p \implies q\)와 동일한 진리값을 지니는 \(\neg p \lor q\)가 달리 보인다.
| \(p\) | \(q\) | \(\neg p \lor q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
위 진리표에서 \(p\)가 T인 경우에는 \(q\)가 T일 때만 T가 된다. 즉, \(p\)가 T라면, \(p \implies q\) 혹은 \(\neg p \lor q\)가 T가 되는 경우는 \(q\)가 T일 때 뿐이다.
공진리
‘공진리(vacuous truth)’, ‘항진’ 혹은 ’공허 참’의 문제를 살펴보고 가자. 얼핏 이해가 쉽지 않을 수 있다. 진리집합으로 보면 상대적으로 이해가 쉽다. \(p\)가 F라는 것은 \(P=\varnothing\)을 의미한다. 집합의 공리에 따르면 공집합은 모든 집합의 부분 집합이다. 따라서 공진리에 속하는 조건 명제는 아무런 의미를 지니지 않지만 형식 논리상 언제나 참이다.
조건 명제의 부정
조건 명제의 ’부정’은 어떻게 될까? 조건 명제를 \(p \implies q\)의 형태로 놓고 부정 명제를 떠올리기는 쉽지 않다. 대신 \(\neg p \lor q\)의 부정 명제를 만들어보자. \(\neg(\neg p \lor q) = p \land \neg q\)가 된다.
직관적으로 생각해보자. 배중률에 따르면 \(p \implies q\)가 성립하지 않는 경우가 단 하나라도 존재하면 해당 부정형이 참이 된다. 즉, \(p\)를 만족하는 경우 중에서 \(\neg q\)를 만족하는 것이 존재하면 된다. 앞서 \(p \implies q\)에서 \(p\)가 \(\forall\)의 전칭 한정기호를 달고 있다면, 조건 명제의 부정형에서 \(p\)는 \(\exists\)의 존재 한정기호 달고 있다. 진리 집합으로 서술하면 \(P \cap Q^C \neq \varnothing\)인 경우에 해당한다.
함수의 극한
누구나 한번쯤 좌절해봤다는 함수 극한, \(\lim_{x \to a} f(x) = L\), 에 관한 “엡실론-델타 논법(epsilon-delta argument)”은 다음과 같다.
엡실론-델타 논법의 정식화는 대략 코시(Cauchy)로 거슬러 올라간다. 그는 \(\epsilon\)을 error의 의미로 \(\delta\)를 distance의 의미로 썼다고 한다. 즉, 목표가 되는 타겟 \(f(x)\)의 ’오차’를 일정한 범위 이하로 줄이기 위해 필요한 \(a\) 주변의 ’거리’로 느슨하게 외우면 괜찮을 듯 싶다.
\(x \in \mathbb R\)인 모든 \(x\)와 모든 \(\epsilon > 0\)에 대해서 다음을 만족하는 어떤 \(\delta > 0\)가 존재한다; \(0 < |x - a| < \delta\) \(\implies\) \(|f(x)-L| < \epsilon\).
영어로는 다음과 같다.
For every \(\epsilon > 0\), there exists a \(\delta > 0\) s.t. for all \(x \in \mathbb R\), \(0 < |x-a| < \delta\) implies \(|f(x)-L| < \epsilon\).
기호만으로 표현해보자.
\((\forall \epsilon >0)(\exists \delta >0)(\forall x \in \mathbb R)(0 < |x-a| < \delta \implies |f(x) - L|<\epsilon)\) \((\forall \epsilon >0)(\forall x \in \mathbb R)(\exists \delta: 0 < |x-a| < \delta \implies |f(x) - L|<\epsilon)\)
하나씩 끊어서 말로 살펴보자.
- \(x=a\) 주변으로 양쪽으로 어떤 \(\delta\) 크기의 구간을 잡는다.
- 해당 구간에 속하는 모든 \(x\)를 고려하자.
- \(x \to a\) 일 때 함수 \(f(x)\)의 극한값을 \(L\)이라고 하자.
- \(\delta\)를 조정해서 \(f(x)\)와 \(L\) 사이의 거리(\(|f(x)-L|\))가 모든 \(\epsilon>0\)보다 작게 만들 수 있다. 즉, 이 조건을 만족하는 \(\delta\)가 존재한다.
양화사(quantifier)에 각별히 주의하자. 명제의 부정을 정의할 때 골치거리가 되는 것이 바로 이 녀석이다.
함수의 극한이 존재하지 않는 경우
이제 함수의 극한에 관한 정의의 부정(negation)을 만들어 보자. 이 부정이 참이 되는 경우, 즉 극한이 존재하지 않는 경우도 함께 살펴볼 것이다. 정의가 함축(implication, \(\implies\))의 형태를 취하고 있으므로 부정을 만들 때 앞서 살펴본 방식을 따르면 된다.
여기서 문제가 되는 것이 양화사다. 질문은 다음과 같다.
- 양화사를 \(p\)와 \(q\)의 조건이 넣어서 함축 명제의 부정을 만들어야 할까?
- 아니면 영화사는 별도로 처리해줘야 할까?
결국 정의의 취지가 무엇인지에 달려 있다. 극한의 정의를 보면 존재하는 세 개의 양화사가 일종의 전제로 제시되어 있다. 따라서 함축과는 별도로 다루는 것이 타당할 것이다. 양화사는 부정을 취하면 반대가 된다. 즉 엡실론-델타 논법에 따른 함수 극한 정의의 부정은 다음과 같다.
모든 \(\delta>0\)에 대해서 다음을 만족하는 어떤 \(\epsilon>0\)와 어떤 \(x \in \mathbb R\)이 존재한다; \(0 < |x-a| < \delta\)와 \(|f(x) - L| \geq \epsilon\)를 동시에 만족한다.
역시 구별해서 풀어보자.
- \(a\)의 모든 주변(\(\delta\)의 크기)에 속한 어떤 \(x\)를 고려하자.모든 \(\delta>0\)이므로 \(a\) 주변의 지극히 극소한(?) 범위에서까지 만족해야 한다. 이것은 매우 강한 조건이다. 원래 정의에서 \(\epsilon\)에 대해서 강한 조건이었다면 이것이 \(\delta\)로 바뀐 셈이다.
- \(|f(x)-L|\) 값을 어떤 \(\epsilon\) 보다 낮게 줄일 수 없는 \(x\)가 존재한다.
이 경우는 \(\lim_{x \to a}f(x)\)는 존재하지 않는다.
여기를 같이 참고하자.
진리 집합
진리 집합으로 다시 따져보도록 하자. 진리 집합은 조건제시법(set builder notation)을 통해 표현한다. 양화사를 함께 표현해보자.
\[ \begin{aligned} P & = \{\forall x>0,~\exists \delta>0 \, \vert ~|x - a| < \delta \} \\ Q & = \{\forall x>0,~\forall \epsilon>0 \, \vert ~|f(x) - L| < \epsilon \} \end{aligned} \]
부정형의 양화사를 적용해보자. 앞서 보았듯이 양화사는 이 명제의 전제 조건이다. 따라서 명제를 부정하면 양화사는 반대로 뒤집히게 된다. 따라서 같은 \(P\)의 진리집합이라고 해도 원래의 명제와 부정형의 명제에는 서로 다른 영화사가 적용된다. \(P\)의 진리 집합에 적용되는 한정사는 \(\forall \delta > 0\)이고, \(Q^C\)에 적용되는 한정 명제는 \(\exists \epsilon > 0\)이다. 원 명제의 진리집합과 구별하기 위해서 아래와 같이 표기해보자. \[ \begin{aligned} \hat P & = \{ \exists x>0, ~\forall \delta>0 \, |~|x - a| < \delta \} \\ \hat Q^C & = \{ \exists x>0, ~\exists \epsilon>0 \, | ~ |f(x) - L| \geq \epsilon \} \end{aligned} \]
조건제시법을 쓸 때 \(|\)과 \(:\)는 차이가 있을까? 별 차이가 없다는 게 중론인 듯 싶다. 영어로 옮기면 “such that(s.t.)”에 해당한다. 사례처럼 “s.t.”이 중복되면 번갈아서 써주면 어떨까 싶다.
만일 \(\hat P \cap \hat Q^C \neq \varnothing\)이면, 정의상 함수의 극한은 존재하지 않는다.
머리 속으로 그림을 그려보자. 모든 \(\delta>0\)에 관해서 \(\hat P \cap \hat Q^C \neq \varnothing\)이 만족하면 극한은 존재하지 않는다. 아래 그림에서 보듯이 \(x\)를 \(a\)에 아무리 가깝게 근접시키더라도 \(|f(x)-L|\)의 크기를 더 줄이기 힘든 어떤 한계가 존재한다면, \(\lim_{x \to a} f(x)\)는 존재하지 않는다.
그림으로 살펴보면
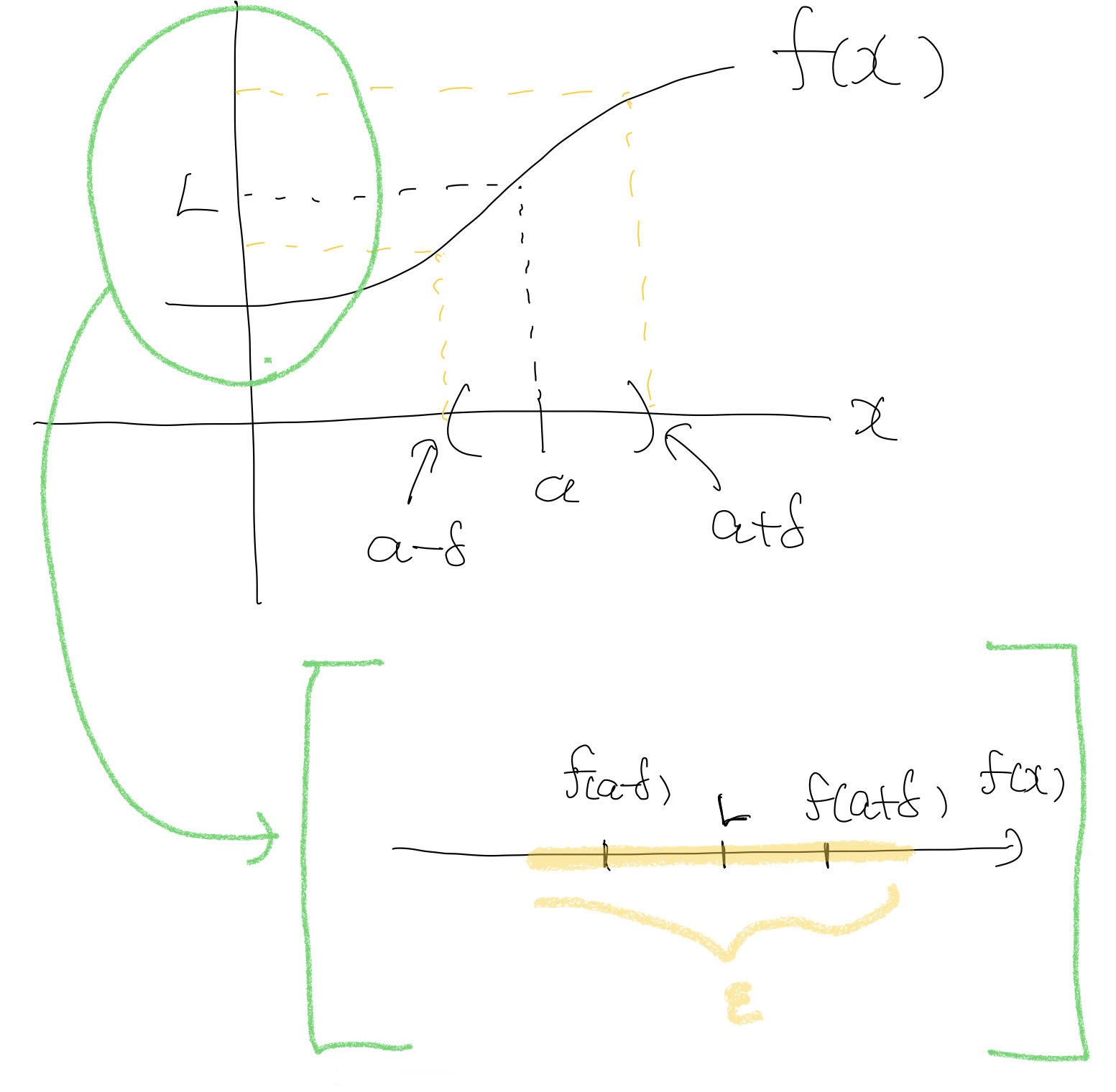
여러가지 상세한 조건을 과감히 생략하고 \(x \in \mathbb R\)에서 정의되는 \(f(x)\)의 그림을 통해 함수 극한을 살펴보기로 하자.
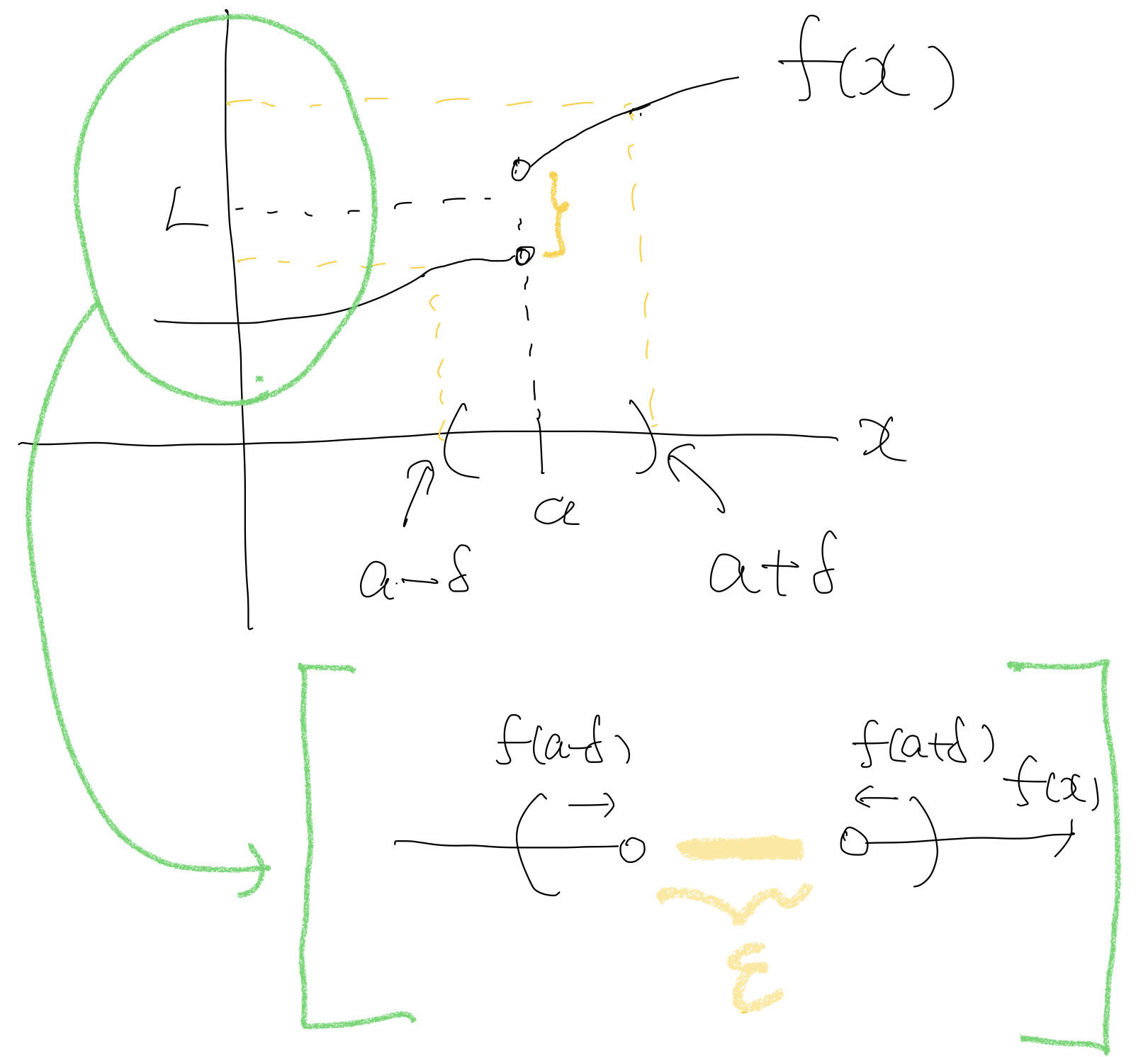
그림이 정확하지는 않지만 이해하는 데 도움이 되지 않을까 싶어 소개한다. 아래 “[ ]”에 있는 그림은 \(y\)축을 옆으로 눕혀 확대해서 그린 것이다. \(f(x)\)가 존재하는 왼쪽의 경우 \(L\) 주변에서 임의의 \(\epsilon\)을 잡더라도 \(\delta\)를 더 작게 설정함으로써 \(|f(x)-L| < \epsilon\) for \(x \in (f(a-\delta), f(a+\delta))\)를 만족한다. 오른쪽의 경우를 보자. \(x=a\)에서 \(f(x)\)의 점프가 있다. 따라서 해당 구간에 적당한 크기의 \(\epsilon\)을 설정하면 \(|f(x)-L| \geq \epsilon\) for \(x=a\)가 모든 \(\delta\)에 대해서 성립한다.
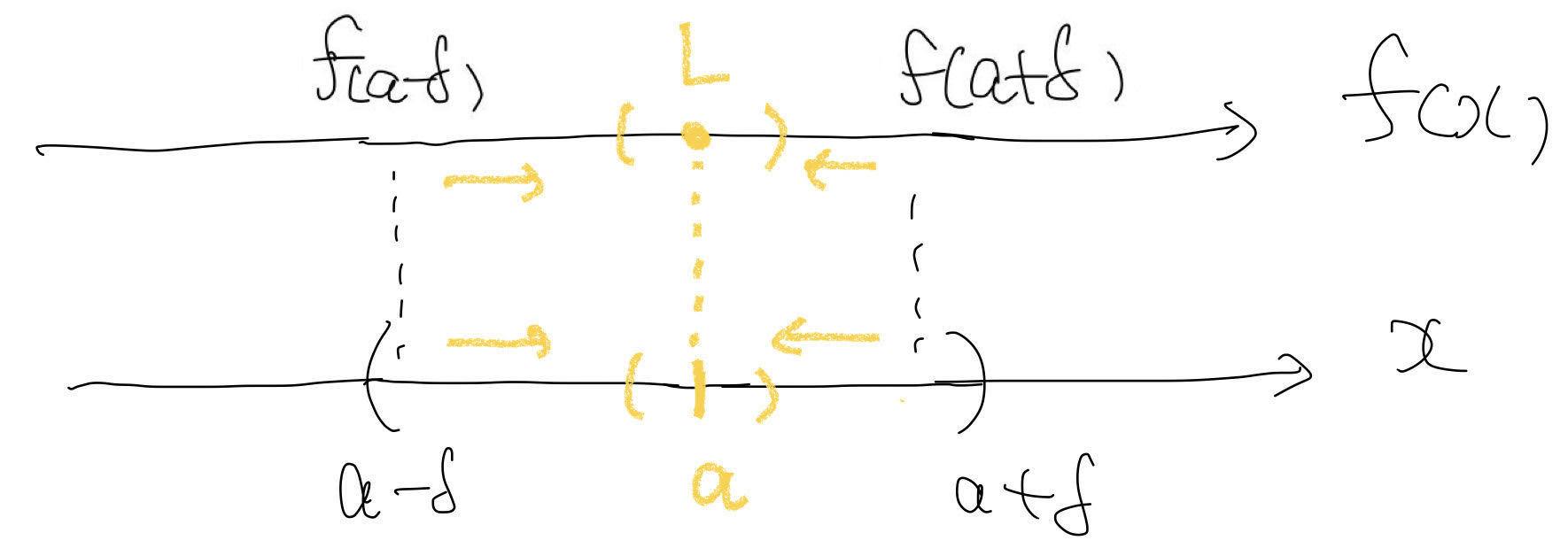
함수의 극한이 존재하는 경우
\(\lim_{x \to a} f(x)\)가 존재하는 경우를 살펴보자. 문장으로는 이상하지만 이렇게 풀어 놓고 써보자.
- \(p\): 다음의 조건을 만족하는 어떤 \(\delta>0\)가 존재한다; \(|x - a| < \delta\)
- \(q\): 모든 \(\epsilon>0\), 모든 \(x \in \mathbb R\)에 대해서 다음 조건을 만족한다; \(|f(x) - L| < \epsilon\)
그림에서 보듯이 어떤 크기의 \(\epsilon\)가 주어진다고 해도 \(\delta\)를 필요한 만큼 작게 택하여 \(f(x)\)와 \(L\)의 거리를 충분히 좁힐 수 있을 때, 함수의 극한값이 존재한다.
다소 동어반복이 될지는 모르겠지만 극한이 존재하지 않는 경우에 넣어서 따져보면 이해에 도움이 된다. 진리집합 \(Q^C\) 즉 \(|f(x) - L| \geq \epsilon\)를 만족하는 \(\epsilon\)와 \(x\)가 존재한다고 하자. \(x\)를 \(a\)에 충분히 붙이게 되면, 즉 \(\delta\)를 충분히 작게 잡으면, 이 조건을 만족하는 \(\epsilon\)은 존재하지 않는다. 즉, \(P \cap Q^C = \emptyset\)이다.
함수의 극한이 존재하지 않는 경우
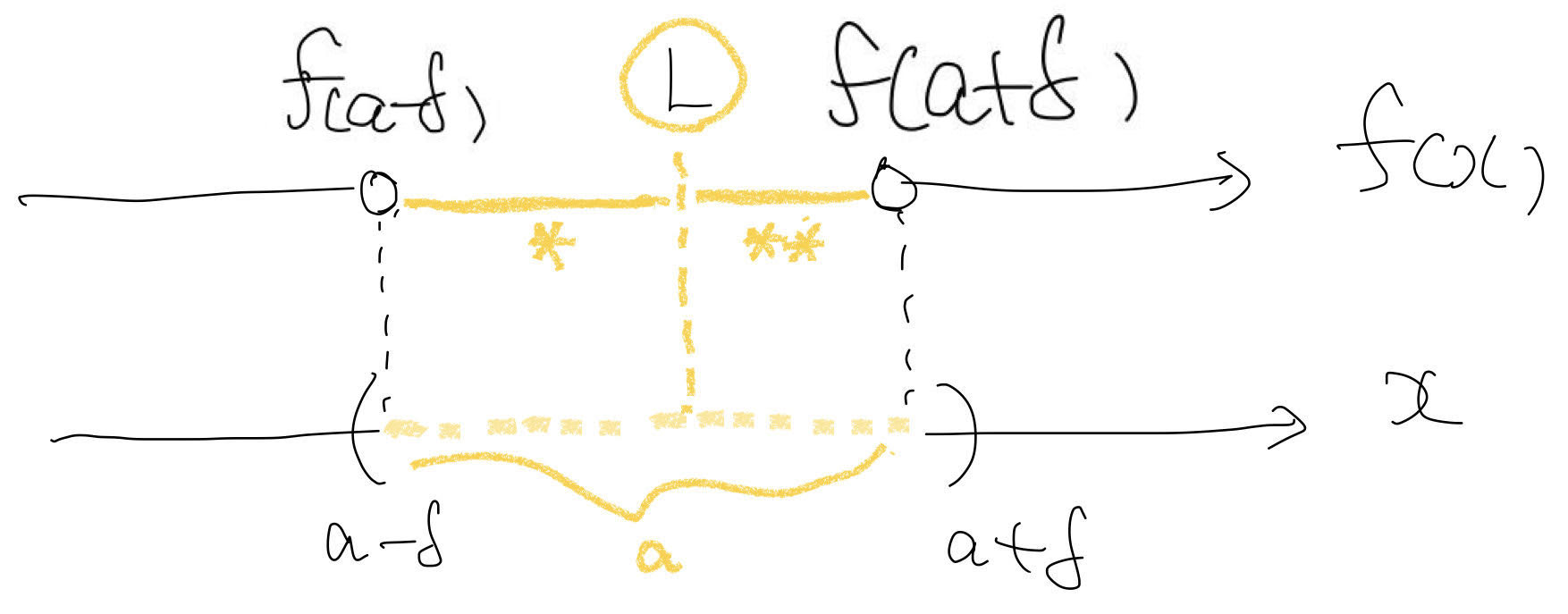
\(L\)이 \((f(a-\delta), f(a+\delta))\) 사이 어딘가에 존재한다고 하자. 이때 \(|L-f(a-\delta)|\)(그림의 *)과 \(|L-f(a+\delta)|\)(그림의 **) 중 작은 값보다 같거나 작은 어떤 값을 \(\epsilon\)이라고 두자. 이때 \(|x-a|<\delta\)를 만족하는 모든 \(\delta\)에 대해서 \(|f(x)-L| \geq \epsilon\)을 만족하는 \(x\)를 찾을 수 있다. 즉, \(P \cap Q^C \neq \emptyset\). 이 상황을 명제로 표현하면 아래와 같다.
\((\exists \epsilon)(\exists x)(\forall\delta>0)\) s.t. \(|f(x)-L| \geq \epsilon\) for \(x \in (a-\delta, a+\delta)\).
\(f(x)\)는 \(x=a\) 주변에서 끊어져 있고, 이 간격과 \(L\)의 위치를 고려해서 모든 \(\delta\)와 \(|f(x)-L| \geq \epsilon\)를 만족하는 \(\epsilon>0\)와 \(x\)를 찾을 수 있다. 위 그림에서 보듯이 \(\delta\)를 아무리 작게 설정해도 \(x=a\)에서 존재하는 \(f(x)\)의 간격을 줄일 수는 없다. 즉, \(\lim_{x \to a} f(x)\)는 존재하지 않는다.
연습 삼아서 \(a\)에서 \(f(x)\)의 극한값이 존재하는 경우도 살펴보자. 위의 그림에서 보듯이 모든 \(\delta\)에 대해서 성립해야 하므로 어떤 \(\epsilon\)이나 \(x\)를 잡더라도 \(\delta\) 를 좁히면 \(|f(x)-L| \geq \epsilon\)의 조건을 깰 수 있다.
My bullshit
엡실론-델타 논법을 어렵게 여기는 이유가 무엇일까? 아마도 극한을 우리가 머리 속에서 떠올리고 말하는 방식 때문이 아닐까 싶다. \(x \to a\)를 표현할 때 흔히 “\(x\)가 \(a\)에 한없이 다가갈 때”라고 말한다. 이 말은 \(x\)가 \(a\)를 향해 끊임없이 (조금씩) 접근하는 동적인 이미지를 떠올리게 한다. 하지만 \(x\)가 \(a\)에 수렴하는 동적인 경로는 셀 수 없이 많다. 이 모든 경로에 대해서 \(f(x)\)가 \(L\)에 수렴하는지를 확인하기는 불가능하다.
극한을 찾고 싶은 점(\(x=a\))의 함수 값에서 아주 미세한 교란이 발생했다고 하자. 이때 다시 원래의 값으로 돌아갈 수 있는 \(x=a\) 주변의 범위를 잡을 수 있는지가 극한 정의의 관심사이다. 어떻게 다시 \(L\)로 돌아갈지는 정할 수도 없고 관심사도 아니다. 함수 주변에서 임의의 교란이 발생했을 때 원래 값을 복원할 수 있는 \(x\)의 범위를 \(a\) 주변에서 정할 수 있다면, \(L\)을 극한으로 보겠다는 것이다.
‘무한히’ 존재할 동적인 수렴을 다룰 수 없으니 이를 정적인 형태로 바꿔 수학적으로 다룰 수 있도록 만든 장치가 엡실론-델타 정의가 아닐까?