RSA, Simply Explained
tl; dr
- RSA 알고리즘을 쉽게 풀어보자.
왜?
한글로 된 책이나 블로그 등을 찾아보면 RSA가 제법 많이 소개되어 있다. 아쉽게도 대체로 개념 혹은 전체적인 그림 정도의 설명이 많았고, 알고리즘을 구체적으로 해설하는 경우는 드물더라. 보안 지식이 일천한 나는 그렇게 느꼈다. 알고리즘 자체를 보다 친절하게 소개하는 내용을 두루 찾다가 아래 두 개의 위키를 찾았다. 나중에 까먹을 나 놈을 위해서 내용을 간단히 정리해두도록 하곘다.
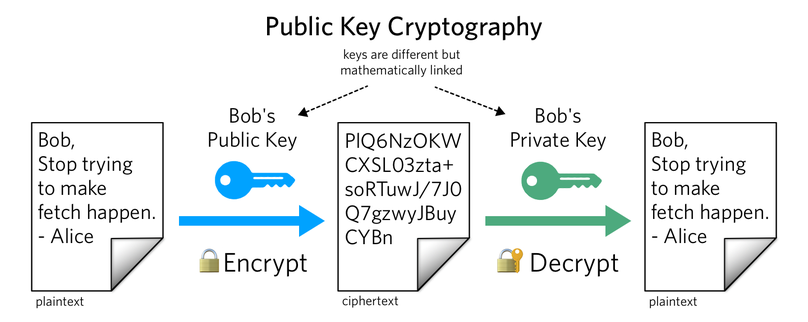
비대칭 암호의 핵심은 공개 키로 어떤 메시지 혹은 내용을 암호화를 하고 이를 개인 키를 통해서 풀 수 있게 (복호화) 하는 것이다. 공개 키는 널리 퍼트리고, 개인 키는 해당 개인이 보유하고 관리한다. 이런 구조 때문에 암호화와 복호화에 필요한 키를 공유하는 대칭 암호 체계에 비해 비대칭 암호가 보안에 우수하다.
만일 암호화를 수행해서 공개 키를 불특정 다수에게 전달하고 개인 키를 갖는 쪽이 sender(센더)면 이는 ’전자 서명’이다. 반대로 receiver(리시버)가 공개 키를 배포하고 자신이 개인 키를 보유한다면, 이는 암호화 기반 메시지 전달이다. 동전의 양면 처럼 동일한 개념이므로 여기서는 후자, 즉 암호화 메시지 교환을 다루도록 하겠다.
개념
RSA 알고리즘의 핵심은 소수의 활용 그리고 오일러 정리다. 필요한 개념 몇 가지 미리 정리하고 가자.
Euler \(\phi\) function
오일러 피 함수(Euler totient function), \(\phi(n)\), 은 \(n\)까지의 정수 중에서 \(n\)와 서로소(coprime)인 정수 집합의 크기를 나타낸다. 오일러 피 함수에 관해서 아래와 같은 내용이 성립함을 확인하자.
- 만일 \(p\)가 소수일 때, \(\phi(p) = p-1\)가 성립한다. \(p\)가 소수라면 정의상 \(1, \dotsc, p-1\)의 모든 수와 \(p\)는 서로소가 된다.
- 만일 \(p,q\)가 서로소이면, \(\phi (pq) = \phi(p) \phi(q)\). 증명이 간단하지 않으니 일단 받아들이자.
증명은 여기를 참고하자.
Euler theorem
\(n\)이 양의 정수라고 하고, \(a\)와 \(n\)은 서로소라고 하자. 이때 아래의 관계가 성립한다.
\[ a^{\phi(n)} \equiv 1~(\text{mod } n) \]
즉, 오일러 정리는 \(n\)에 관한 오일러 피 함수와 \(n\)의 나머지 연산 간에 매우 편리한 관계를 보여준다. 오일러 정리애 관한 증명 역시 생략한다.
증명은 여기를 참고하자. 증명이 몹시 난해한 것은 아니다.
잠깐 “나머지 연산”(modulo operation)이 왜 동원되는지 살펴보고 넘어가자. 나머지 연산을 통해 일방향 함수를 쉽게 구성할 수 있다. \(f(x) = ax\)가 있다고 하자. \(x\)를 알면 \(f(x)\)를 쉽게 계산할 수 있고 반대로 \(f(x)\)를 알면 \(x\)도 쉽게 구할 수 있다. 이런 함수를 양방향 함수라고 한다. 반면, \(f(x) = a^x\text{ mod ($b$)}\)라고 하자. 이때, \(a, b\)가 주어진 값이라고 하자. \(x\)를 알면 쉽게 \(y\)가 계산된다. 반면, \(f(x)\)가 주어졌다고 해도 \(x\)를 알아내기는 쉽지 않다. 하나씩 다른 값을 넣어보면서 맞는지 확인하는 방법 밖에 없다. 일방향 함수에서는 \(a^x\)와 \(b\)가 충분히 큰 값일 때, \(f(x)\)를 알아도 \(x\)를 찾기 쉽지 않다.
이런 형태의 문제를 이산 대수의 문제라고 한다.
Step by Step
여기서는 암호화를 수행하는 쪽이 리시버인 상황을 상정해서 설명하겠다. 리시버는 나에게 온 메시지가 나에게 온 것이 맞는지 그리고 메시지를 나만 볼 수 있는지가 염려된다. 이를 보장하기 위해서 리시버는 아래와 같은 과정을 통해서 공개 키 정보를 대중에게 제공한다.
- 리시버는 \(p\), \(q\) 두 개의 (상대적으로 큰) 소수를 생성한다. 값은 필요한 만큼 커야 한다. \(p \cdot q=n\)이 된다. \(p\), \(q\)는 당연히 비공개 정보여야 한다. 하지만 \(n\)은 공개 키가 된다. \(n\)으로부터 \(p\), \(q\)를 찾는 것은 단순 무식한 작업(brute force)을 요하고, 그래서 암호로서 기능할 수 있다.
- \(\phi(n) = \phi (pq) = (p-1) (q-1)\) 이 성립한다. 만일 \(\phi(n)\)을 알고 있으면 \(p+q\)을 알게 된다. \(pq=n\)을 알고 있으므로 이차 방정식을 풀면 \(p\), \(q\)를 알게 된다. 따라서 \(\phi(n)\)은 비공개 정보다. 오일러 피 함수에 해당하는 공개 키를 만들기 위해서 \(\phi(n)\)과 서로소인 \(e\)를 하나 생성하도록 하자. 대신 이 녀석이 공개 키가 된다.
- \(\phi(n)\)의 나머지 연산에 대해서 \(d e = 1\)을 만족하는 \(d\)를 구하자. 이 녀석이 비밀 키가 된다.
\(\phi(pq) = \phi(p)\phi(q)\)가 성립한다. \(p\), \(q\)는 각각 소수이므로 \(\phi(p)=p-1\), \(\phi(q)=q-1\)이다. 한편, \(e\)는 대체로 공개 키의 크기 역할을 한다. 따라서 \(2^{16}+1\)이 자주 사용된다.
이제 공개 키와 비밀키를 한번 나누어 써보도록 하자.
| secret | public |
|---|---|
| \(p, q\) | \(n\) |
| \(\phi(n), d\) | \(e\) |
리시버는 공개 키 \(n\), \(e\)를 일반에게 공개한 상태다.
- 이 리시버에게 메시지를 보내고자 하는 센더는 자신의 메시지 \(m\)을 공개 키 \(e\)를 통해 암호화한다. 이 과정은 별게 아니다. 메시지 혹은 메시지의 해시값에 \(e\) 승을 한 값에 \(n\)의 나머지 연산을 적용한다. 즉,
\[ c \equiv m^e ~ (\text{mod } n) \]
- 아래에서 보듯이 \(n\)이 너무 크면 나머지 연산이 제대로 적용되지 않는다. 또한 \(e\)의 값이 너무 크면 계산 과정이 길고 복잡해진다.
- 메시지를 메시지 자체라고 생각할 필요는 없다. 메시지의 해시값이라고 생각하면 암호화의 대상이 되는 메시지는 원 메시지보다 훨씬 짧을 수 있다. 리시버와 센더가 맞춰봐야 하는 것은 해당 해시값이다.
- 리시버는 암호화된 메시지를 받은 후에 여기에 \(d\) 승을 하고 나머지 연산 \(n\)을 적용한다. 즉,
\[ c^d \equiv m~(\text{mod } n) \]
위에 보는 것처럼 두 번의 나머지 연산에서 센더는 \(n\), \(e\)의 공개된 정보(공개 키)만을 활용했고, 리시버는 복호화 과정에서 자신이 갖고 있는 정보, 개인 키 \(d\)를 활용했다.
증명
오일러 정리를 활용하면 위 연산을 쉽게 증명할 수 있다.
- 오일러 정리에 따르면, \(m^{\phi(n)} \equiv 1~(\text{mod } n)\)이 성립한다.
- 우리는 \(d\)와 \(e\)를 고를 때 \(d e \equiv 1~(\text{mod }\phi(n))\)이 되도록 골랐다. 따라서 \(de = k \phi(n) + 1\)이 되는 적절한 \(k\)가 존재한다는 뜻이다.
이를 정리하면,
\[ \begin{aligned} m^{de} & \equiv m^{k \phi(n)+1} \\ & \equiv m^{k \phi(n)} m \\ & \equiv (m^\phi(n))^k m \\ & \equiv 1^k m ~(\text{mod } n) \end{aligned} \]
공개 키인 \(n\)과 \(e\)를 생성하는 과정을 보자. 생성 과정에서 일방향 연산, (충분히 큰) 소수 및 서로소를 활용했다. 따라서 공개 키만으로 암호화에 동원된 \(p, q, \phi (pq), d\)를 빠른 시간 내에 쉽게 알아낼 수 없다. 이것이 암호화가 의도하는 것이다.