Cantor’s Theorem
Prelim
Cardinality
집합이 ’크다’는 것의 의미를 따져보자. 유한 집합의 경우 원소의 개수에 따라서 크기가 정해지므로 그 뜻이 자명하다. 그러면 무한 집합의 크기는 어떻게 비교할 수 있을까? 무한 집합에 대해서는 원소의 ’개수’라는 개념을 쓸 수 없다. 대신 크기의 비교를 위해서 카디널 수(cardinality)라는 개념을 쓴다. 무한 집합 \(A\)에 대해서 \(|A|\)라고 쓸 경우 이는 무한 집합의 크기, 즉 카디널 수를 의미한다.
자세한 내용을 생략하면 두 집합 사이에 일대일 대응 함수가 존재할 경우 같은 카디널 수를 지닌다고 말한다. 그리고 자연수 집합(\(\mathbb N\))은 가장 작은 무한 집합으로 정의한다.
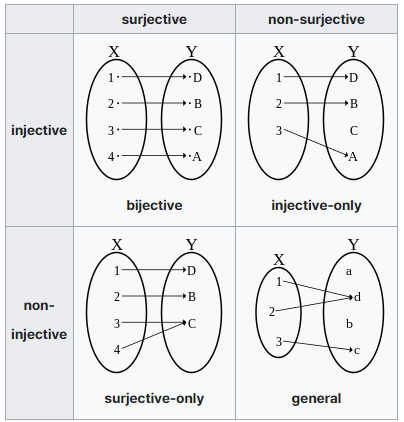
Injection, Surjection, and Bijection
앞서 보았듯이 집합의 크기를 재려면 집합과 집합 사이에 어떤 짝짓기(mapping)가 가능한지를 살펴야 한다. 용어 및 번역어 먼저 정리하자.
- 전사 함수(surjective function): onto function
- 단사 함수(injective function): 일대일 함수(one-to-one function)
- 전단사 함수(bijective function): 일대일 대응(one-to-one correspondence) one-to-one and onto
“일대일 함수”와 “일대일 대응”은 단사 함수와 전단사 함수를 각각 뜻한다. 용어에 주의하자.
고등학교에서 함수를 배울 때 “전사 함수”, “단사 함수”와 같은 구별이 필요한 이유는 별로 강조하지 않는다. 이러한 분류가 카디널 수를 따질 필요하다는 것을 미리 알았다면…
단사 함수의 경우 정의역 \(X\)가 치역 \(f(X)\) 보다 ‘크지’ 않아야 존재할 수 있다. 전사함수가 존재하려면 반대로 \(f(X)\)가 \(X\) 보다 크지 않아야 한다. 해당 함수가 존재할 수 있는 정의역과 치역의 크기에 관한 필요 조건은 다음과 같다.
- 전사 함수: \(|X| \geq |f(X)|\)
- 단사 함수: \(|X| \leq |f(X)|\)
- 전단사 함수: \(|X| = |f(X)|\)
Theorem
이제 칸토어의 정리를 살펴보자. 정리의 대단한 내용을 생각하면, 증명은 매우 간단하다. 임의의 집합 \(A\)에 대해서 멱집합 \(\mathcal P (A)\)는 \(A\)보다 크다. 즉,
\[ |\mathcal P(A)| > |A|. \]
Proof
\(A\)가 유한 집합일 때는 자명하다. 즉, \(N < 2^N\) for \(N \in \mathbb N\)이 성립한다. 이하에서는 \(A\)가 무한 집합이라고 전제한다.
Part 1
\(|A| \leq |\mathcal P (A)|\)를 증명하자. 이는 \(f: A \to \mathcal P(A)\)를 만족하는 단사 함수, 즉 일대일 함수가 존재하면 된다. \(\mathcal P(A)\)에는 \(a \in A\)의 \(\{ a \}\)가 존재한다. \(f(x) := \{ x \}\)는 \(X \to f(X)\)인 단사 함수이다.
Part 2.1
\(|A| \neq |\mathcal P (A)|\)
이는 귀류법(proof by contradiction)을 활용한다. 양변의 카디널 수가 같은 경우, 즉 전단사 함수가 존재한다고 가정하자. 여기 속하는 함수 \(f: A \to \mathcal P(A)\)는 전사 함수이다. 이제 다음과 같은 집합 \(B\)를 빚어보자.
\[ B = \{ x \in A| x \notin f(x) \} \]
\(B\)는 \(x \in A\)에는 들어 있지만 \(f\)에 의해 부분 집합의 집합으로 짝지어진(mapping) 원소(이 원소는 ’집합’이다)에는 속하지 않은 집합 \(A\)의 원소로 구성된 집합이다.
예를 들어보자. \(A = \{1,2,3\}\)일 때, \(1 \to \emptyset\), \(2 \to \{ 1, 3\}\), \(3 \to \{ 2\}\)와 같은 짝짓기를 의미한다.
\(B\)는 \(A\)의 원소들로 구성되어 있으므로 당연히 \(B \in \mathcal P(A)\)이다. \(f\)는 가정에 따라서 전사 함수이다. 따라서 \(\mathcal P(A)\)에 속한 모든 원소에 대응하는 \(a \in A\)가 반드시 존재한다. 이때 집합 \(B\)에 대응하는 \(A\)의 원소를 \(a\)라고 하자. 즉, \(f(a) = B\)인 \(a \in A\)가 존재한다.
Part 2.2
\(a\)는 \(B\)에 속하거나 혹은 그렇지 않거나 둘 중 하나는 참이어야 한다. 각각의 경우를 살펴보자.
- \(a \in B\); 이 명제가 맞다면, \(a \in f(a)\)가 성립한다. 그런데 집합 B의 정의(\(B\)의 such that)에 따르면 \(a \notin f(a) = B\)이다; \(a \notin B.\) 따라서 모순이다.
- \(a \notin B\); 이 명제가 맞다면, \(a \notin f(a)\)가 성립한다. 그런데 집합 \(B\)의 정의에 따르면 \(a \notin f(a)\)는 B의 원소다; \(a \in B.\) 따라서 모순이다.
두 경우 모두 모순이다. 귀류법에 따라 \(|A| \neq |\mathcal P(A)|\)가 참이다. 앞서 단사함수의 존재 증명과 함께 집합의 카디널 수에 관해 칸토어의 정리가 성립한다;
\[ |A| < |\mathcal P (A)|. \]
Simple but Beautiful
이 정리 참 아름답다. ‘전사 함수’ \(f(X)\)에 짝지워진 치역에 존재하는 어떤 원소를 폭탄 삼아 잘못된 전제에서 출발한 명제를 폭파시키는 방식의 절묘한 논법이다. 자세히 보면 이 정리는 러셀의 역설과 꽤 닮았다. 러셀이 칸토어의 해당 정리를 먼저 봤다고 하니, 레셀의 아이디어가 칸토어에서 왔다고 볼 수도 있을 듯 싶다. 러셀의 역설이 칸토어의 소박한 집합론에 일격을 날린 것을 생각하면 조금 아이러니한 대목이다.
소박한 집합론(naive set theory)은 일정한 서술적 특성을 바탕으로 집합을 (쉽게) 정의할 수 있다고 보았다. 러셀의 역설은 이러한 공리에 구멍이 있음을 보여준다. 다소 말장난 같지만 생각해볼 대목이 있다. 직관적으로 생각해보자. 자신을 포함해 모든 것들의 ’집합’이 가능할까? 가능하다고 가정해보자. 이 집합에는 그 자신이 포함될 것이다. \(x \in x\)가 된다. 이제 \(R = \{ x: x \notin x \}\)라고 하자. 이 집합 역시 일정한 서술적 특성에 기반하고 있으므로 소박한 집합론에 따르면 집합이 될 수 있어야 한다. 이렇게 함정이 완성된다.
이제 \(R \in R\)을 만족한다고 하자. 그런데 \(R\)의 정의상 \(R \notin R\)이어야 한다. 따라서 모순이다. 만일 \(R \notin R\)이라고 하자. \(R\)의 정의상 \(R \in R\)이어야 한다. 따라서 모순이다. 소박한 집합론의 주장과 달리 집합으로 정의될 수 없는 특징 혹은 대상이 존재함을 러셀의 역설이 보여준 셈이다.
조금 말로 풀어보자. 모든 것을 포함하는 집합이 존재한다면, 그 자신을 포함하지 않는 집합을 정의할 때 문제가 생긴다. 러셀의 역설의 사례로 많이 언급되는 경우들이 거의 이런 재귀적인 특징을 지니고 있다. 마을에 존재하는 유일한 이발사 “갑”은 스스로 이발을 하지 않는 모든 사람을 이발하는 사람이다. 그렇다면 이발사 갑은 자신을 이발할 수 있는가? 할 수 없다. 그는 스스로 이발을 하지 않는 모든 사람을 이발하기 때문이다. 그렇다면 남에게 이발을 부탁할 수 있는가? 그럴 수도 없다. 스스로 이발을 하지 않는 모든 사람을 이발해야 하기 때문이다.
보다 상세한 내용은 여기를 참고하자.