Dot Product with Geometry
TL; DR
- 닷 프로덕트 혹은 내적을 기하적으로 이해하면 여러모로 편리하고 기억에도 잘 남는다.
Definition
dot product는 내적이라고도 번역하지만 여기서는 닷 프로덕트로 쓰기로 하겠다. 먼저 정의부터 살펴보자.
\[ \mathbf{u}=\left[u_{1}, {u}_{2}, \ldots, {u}_{n}\right] \in {\mathbb R}^n \]
\[ \mathbf{v}=\left[{v}_{1}, {v}_{2}, \ldots, {v}_{n}\right] \in {\mathbb R}^n \]
\[ \mathbf{u} \cdot \mathbf{v} = \sum_{n} u_i v_i \]
쉽게 말해서 닷 프로덕트는 차원이 같은 두 개의 인풋 벡터를 하나의 스칼라로 바꿔주는 일종의 함수로 이해할 수 있다. 두 개의 벡터를 서로 연관 짓는데 이를 해당 벡터의 길이라는 정보로 압축한다고 보면 얼추 맞을 듯 싶다. 하나의 숫자로 요약된다는 뜻에서 스칼라 프로덕트라고도 불린다. 그림으로 나타내면 아래와 같다.
From Definition to Geometry
닷 프로덕트에 관한 설명은 정의에서 바로 코사인 법칙으로 넘어간다. 하지만 뭔가 분명하지 않다. 이걸 조금 더 풀어보자.
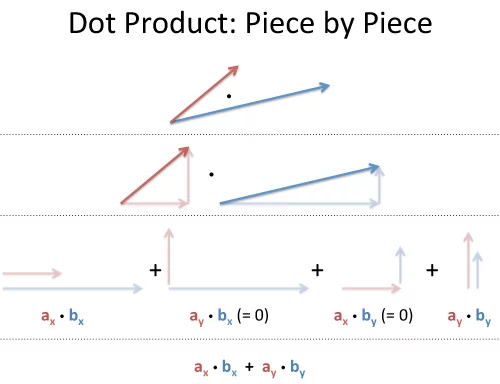
위 그림은 \(2 \times 2\) 벡터의 닷 프로덕트를 각 요소로 분해한 것이다. 이중에서 \(\dfrac{\pi}{2}\) 각을 이루고 있는 벡터는 서로 곱하면 0이 된다. 따라서 닷 프로덕트 계산에서는 \(a_x b_x\)와 \(a_y b_y\)가 남게 된다.
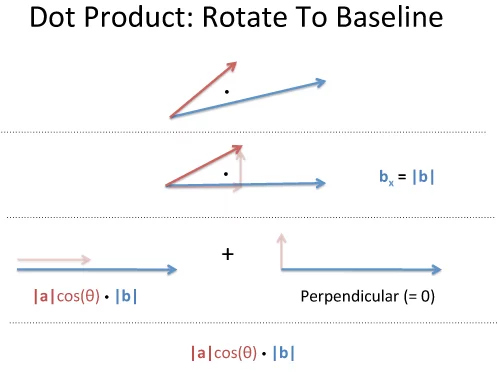
닷 프로덕트란 길이만 문제가 되므로 두 벡터를 한 방향으로 정렬하자.이렇게 되면, 파란색 높이가 \(0\)이 된다. 따라서 위 그림과 같은 코사인 법칙이 쉽게 도출된다.
그림에서 보듯이 벡터를 회전해도 닷 프로덕트의 크기가 변하지 않을까? 여기서 보듯이 임의의 각도 \(\theta\)로 회전해도 닷 프로덕트의 크기는 변하지 않는다.
Symmetry
\(\mathbf{v}\) 벡터를 \(\mathbf u\) 벡터 위에, 즉 \(\mathbf u\) 벡터를 스크린로 삼아 직각으로 쏜 \(\mathbf v\)의 프로젝션 벡터 \(\mathrm{Proj}_{\mathbf u} {\mathbf v}\)의 길이와 \(\mathbf u\) 길이를 곱하면 그것이 \(\mathbf u\)와 \(\mathbf v\)의 닷 프로덕트가 된다. 어느 벡터로 프로젝션 하는지는 관계가 없다. 즉,
\[ {\mathbf v} \cdot {\mathbf u} = \Vert \mathbf u \Vert \Vert {\rm Proj}_{\mathbf u} {\mathbf v} \Vert = \Vert \mathbf u \Vert (\Vert \mathbf v \Vert \cos\theta) \]
\[ {\mathbf u} \cdot {\mathbf v} = \Vert \mathbf v \Vert \Vert {\rm Proj}_{\mathbf v} {\mathbf u} \Vert = \Vert \mathbf v \Vert (\Vert \mathbf u \Vert \cos\theta) \]
다시 보면, 닷 프로덕트의 정의상 \({\mathbf v} \cdot {\mathbf u} = {\mathbf u} \cdot {\mathbf v}\)인 셈이다. 닷 프로덕트는 어떻게 도출하는가? 그 기하학적인 구조는 무엇인가?
With ‘Law of Cosine’
코사인 법칙을 활용해서 닷 프로덕트를 도출할 수 있다. 맨 처음 그림에서 보듯이 벡터 \(\mathbf u - \mathbf v\)와 \(\mathbf u\), \(\mathbf v\)는 삼각형을 이룬다. 따라서 코사인 법칙에 따라서 아래와 같이 적을 수 있다.
여기를 참고 했다. Law of Cosine도 참고하자.
\[ \lVert \mathbf u - \mathbf v \rVert^2 = \lVert \mathbf u \rVert^2 + \lVert \mathbf v \rVert^2 - 2\lVert \mathbf u \rVert \lVert \mathbf v \rVert \cos \theta \]
노름(norm, 길이)에 대해서는 대칭과 쌍방선형이 유지되기 때문에 아래와 같이 쓸 수 있다.
\[ \lVert \mathbf u - \mathbf v \rVert^2 = ( \mathbf u - \mathbf v) \cdot ( \mathbf u - \mathbf v ) = \lVert \mathbf u \rVert^2 + \lVert \mathbf v \rVert^2 - 2 (\mathbf u \cdot \mathbf v) \]
따라서
\[ \mathbf u \cdot \mathbf v = \lVert \mathbf u \rVert \lVert \mathbf v \rVert \cos \theta = \lVert \mathbf u \rVert ( \lVert \mathbf v \rVert \cos \theta) = \lVert \mathbf u \rVert \rVert \text{Proj}_{\mathbf u} \mathbf v \lVert \]
한편 반대로 \(\mathbf u\)에서 \(\mathbf v\)로 프로젝션하는 경우를 생각해 볼 수도 있겠다.
\[ \mathbf u \cdot \mathbf v = \lVert \mathbf u \rVert \lVert \mathbf v \rVert \cos \theta = \lVert \mathbf v \rVert ( \lVert \mathbf u \rVert \cos \theta) = \lVert \mathbf v \rVert \rVert \text{Proj}_{\mathbf v} \mathbf u \lVert \]
닷 프로덕트로 둘 중 어느 쪽을 써도 좋다.
Applications
Cosine similarity
두 개의 벡터가 얼마나 유사한지를 나타내는 지표로 코사인 유사도라는 게 있다. 위에서 보듯이 두 개의 벡터(\(\mathbf v, \mathbf u\))가 이루는 각 \(\theta\)의 코사인 값은 다음과 같다.
\[ \cos \theta = \dfrac{\mathbf u \cdot \mathbf v}{\lVert \mathbf u \rVert \lVert \mathbf v \rVert} \]
두 벡터가 가까울수록 코사인 값이 1에 가깝게 될 것이고, 멀수록 -1에 가깝게 될 것이다. 이른바 코사인 유사도는 이 값의 크기를 따른다. 벡터로 표현된 두 대상 사이의 유클리드 거리와 무관하게 지향하는 방향에 따른 유사도를 측정할 때 이 값을 쓴다.
Hyperplane
닷 프로덕트를 이해하고 있으면 기하학 문제를 쉽게 풀 수 있는 게 많다. 가장 좋은 예가 초평면(hyperplane)이다. 예를 들어 3차원 공간에서 점 \(\mathbf{x}^0 = (x_1^0, x_2^0, x_3^0)\)를 지나면서 벡터 \(\mathbf{p} = (p_1, p_2, p_3)\)에 수직인 평면을 찾고 있다고 하자. 복잡해보이지만 닷 프로덕트를 활용하면 쉽게 풀린다. 즉,
\[ \mathbf{p} \cdot (\mathbf{x} - \mathbf{x}^0) = 0 \]
평면 \(\mathbf x\)가 \(\mathbf{x}^0\)를 지나는 것은 분명하다. 이 평면이 \(\mathbf{p}\)에 수직이라는 것은 두 벡터의 닷 프로덕트가 0이 되면 된다.
Appendix: Geometrically
기하적으로 도출하는 보다 복잡한 방법도 있다. 이해를 돕기 위해서 2차원 벡터공간으로 한정해서 논의하겠다. \(n\) 차원으로 확대하는 것이 수학적으로 어렵지는 않다.
보다 상세한 내용은 여기를 참고하라.
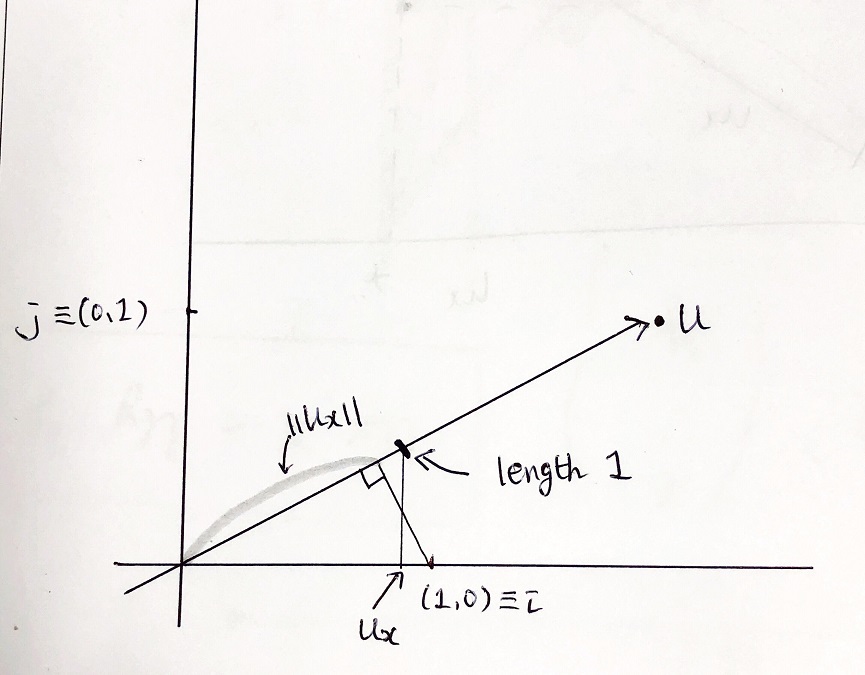
일단 \(\mathbf u\)가 길이 1로 표준화된 벡터라고 정의를 살짝 바꾸겠다. 즉, 새로운 \(\mathbf u\)는 \(\rVert \mathbf u \lVert\)로 \(\mathbf u\)를 나눈 벡터다. 아래 그림처럼 이 벡터를 향해서 2차원 평면의 기저를 구성하는 \((1,0)(\equiv i)\)과 \((0,1)(\equiv j)\)에서 벡터로 프로젝션을 해보자.
이렇게 프로젝션을 하면 프로젝션된 지점의 \(x\) 좌표는 공교롭게도 원점에서부터 해당 프로젝션된 지점까지의 벡터의 길이가 된다. \(y\)에 대해서도 마찬가지다.
이제 (1,1)에서 벡터 \(\mathbf u\)로 프로젝션을 해보자. (1,1)은 각각 두 개의 기저를 1의 가중치로 선형결합한 벡터다. 이 벡터의 프로젝션의 길이는 어떻게 구성될까? 그림에서 보듯이 \(u_x + u_y\)가 된다. 이를 일반적인 논리로 확장해보자. 어떤 임의의 벡터 \(\mathbf v(=(x,y))\)가 존재할 때 해당 벡터는 각각 두 개의 기저의 선형 결합으로 이해할 수 있다.
따라서 \(\mathbf v\) 벡터를 \(\mathbf u\)로 프로젝션한 길이는 다음과 같다.
\[ \underset{\mathbf u 프로젝션}{\left[\begin{array}{ll}{u_{x}} & { u_{y}}\end{array}\right]}\left[\begin{array}{l}{x} \\ {y}\end{array}\right]= u_{x} \cdot x + u_{y} \cdot y = \mathbf u \cdot \mathbf v \]
벡터를 기저의 선형결합을 통해 나타낼 수 있듯이, 벡터의 프로젝션의 길이 역시 비슷한 방식의 선형결합을 동원해서 나타낼 수 있다. 앞서 \(\mathbf u\)가 표준화된 벡터라고 했다. 따라서 원래대로 돌려 놓으면 닷 프로덕트는 프로젝션된 지점까지의 벡터의 거리와 해당 벡터의 길이의 곱이 된다. 즉,
\[ \mathbf u \cdot \mathbf v = \rVert \mathbf u \lVert \rVert \text{Proj}_{\mathbf u} \mathbf v \lVert \]