Shannon’s Entropy
TL; DR
- 섀넌의 (정보) 엔트로피에 대해서 궁금했던 것들
이 글은 왜 쓰나?
섀넌의 엔트로피는 일상적으로 쓰고 중요한 개념이지만 정작 그 개념의 핵심이 뭔지 잊을 때가 있다. 내가 지금 그 꼴이고 그래서 정리 삼아서 포스트를 하나 남겨 보겠다. 미리 밝혀두겠다. 섀넌의 엔트로피와 그 역사적 의미 등 대해서는 좋은 책도 많고 구글링을 하면 이 글보다 좋은 자료가 많이 나온다. 이런 부분을 여기서 반복하지는 않겠다.
섀넌이 어떻게 이 개념을 “엔트로피”라고 이름 붙이게 되었을까? 일설에 따르면 섀넌은 ‘정보’ 혹은 ’불확실성’이라는 명칭이 여러 가지 이유로 적절하지 않다고 생각했다. 당시 섀넌이 조언을 구했던 폰 노이만이 이 개념을 “엔트로피”라고 불러야 한다고 말했다고 한다. 이유는 두 가지다. 우선 ’섀넌의 엔트로피’가 통계물리학에 이미 있는 개념이고 그 명칭이 “엔트로피”이다. 둘째, 이 개념을 제대로 아는 사람이 없을 것이므로 논쟁에서 네가 우위를 점할 수 있다. 츌처
정의
섀넌의 정보 엔트로피 \(H(X)\)의 정의는 다음과 같다. \(X\)는 확률 변수라고 하자. \(\chi\)는 적절한 임의의 가측 집합을 뜻하는데, 일단 넘어가도록 하자.
약간을 사설을 늘어놓자면, 확률 변수는 사건으로 존재하는 실험 집합(sample space)을 실수 공간으로 옮겨 두는 함수다. 이렇게 옮겨진 실숫값은 확률 분포를 지니게 되고 이를 통해 여러 가지 계산을 도모할 수 있다.
\[\begin{align*} H(X) &= \sum_{x \in \chi} p(x) \log \dfrac{1}{p(x)} = -\sum_{x \in \chi} p(x) \log p(x) \\ & = \mathbb E [\dfrac{1}{\log p(x)}] = - \mathbb E [\log p(x)]\\ \end{align*}\]
\(\mathbb E(\cdot)\)의 표현이 보여주듯이 \(H(X)\)는 \(\log \frac{1}{p(x)}\)의 기댓값이다. 이 녀석을 먼저 들여다보자. \(\log \frac{1}{p(x)}\)는 확률 변수 \(X\)에서 \(x\)에 대응하는 사건이 일어날 확률이 주는 ’놀라움’의 크기로 해석할 수 있다. \(p(x)=1\)인 사건은 놀랍지 않다. 확실히 일어나는 사건이기 때문이다. 반면 일어날 확률이 높지 않은 사건은 놀라운 사건이다. 따라서 이러한 놀라움의 정도는 \(\frac{1}{p(x)}\)로 측정할 수 있다. 여기에 계산의 편의성을 위해서 \(\log\)를 취한다. 이렇게 계산된 기댓값이 섀넌의 엔트로피다.
경제학에서 불확실성 하의 선택에서 사용하는 효용함수를 떠올려보자. 위험 기피적인 선호를 지닌 사람의 선호로 흔히 활용하는 것이 \(\log(\cdot)\)다. 불확실성 하의 선호를 처음 연구했던 사람이 폰 노이만와 모르겐스테른인데, 이들은 섀넌과 비슷한 시기에 활동했던 사람들이다. 모종의 평행이론일까?
엔트로피, 즉 무질서의 정도라는 말이 함축하듯이 주어진 확률 변수의 구조가 무작위일수록 엔트로피가 클 것이다. 반면 확률 변수의 구조가 무작위에서 멀어질수록 엔트로피가 줄어든다. (공정한) 동전 던지기와 (공정한) 주사위 던지기를 생각해 보자. 어느 쪽이 엔트로피가 클까? 주사위 던지기 쪽이 크다. 확률이 각각 1/2, 1/6로 같다면 \(H\)를 결정하는 것은 \(\log_{2} {2}\)과 \(\log_{2} {6}\)이 된다. 보다 직관적으로 말해보자. 공정한 동전 던지기는 앞면 아니면 뒷면이다. 공정한 주사위는 6가지 경우의 수가 나온다. 후자의 불확실성, 즉 무질서한 정도가 더 크다.
정보 엔트로피는 왜 유용할까?
정보가 확률적으로 제공된다고 하자. 이 말은 정보를 일종의 확률 분포를 통해 이해하겠다는 뜻이다. 영어로 된 책이 한 권이 있다고 하자. 이 책에 들어 있는 알파벳의 분포를 떠올려 보자. 확률 분포로 본 정보가 어느 정도의 다양성을 지니고 있는지를 요약하는 지표가 섀넌의 엔트로피다. 이 정보가 왜 중요할까? 앞서 말한 책을 디지털로 인코딩하는 작업을 떠올려보자. 어떻게 하면 보다 효율적으로 책의 정보를 가공할 수 있을까? 구체적으로 예를 들어보자.
ABCD가 동일한 비율로 존재하는 정보가 있다고 하자. 이 정보를 디지털로 인코딩하려면 2비트를 사용하면 된다. 2비트로 인코딩할 수 있는 경우의 수가 4가지이기 때문이다. A는 00, B는 01, C는 10, D는 11로 인코딩할 수 있다.
이제 (실제의 알파벳 정보가 그렇듯이) ABCD로 구성된 정보가 다른 분포를 지닌다고 해보자. A는 0.5, B는 0.25, C와 D는 0.125의 확률로 분포한다. 이 정보를 디지털로 인코딩하려면 얼마나 많은 비트를 사용해야 할까? 2비트로 할 수도 있지만 이는 일종의 낭비다. 70%가 A라면 이 녀석을 더욱 간단하게 인코딩하고 비트 크기를 아낄 수 있다. 예를 들어, A는 1, B는 01, C와 D는 각각 001, 000으로 인코딩한다고 해보자. 이 인코딩은 비트를 절약해줄까? 그렇다.
비트를 왜 위와 같은 방법으로 쪼갰을까? 만일 두 자리로 고정된 비트를 인코딩에 활용한다면 마디에 대한 고민을 할 필요가 없다. 그러나, 위 사례처럼 정보를 아끼기 위해서 자리 수가 변하는 비트를 활용한다면 마디와 마디를 구별해야 한다. 이때 위와 같이 정보를 인코딩하면 마디 구분이 별도로 필요 없다. 앞 정보를 처리한 후 1 나오면 A다. 01이 들어오면 B이고 00이 나오면 다음 자리가 1인지 0인지에 따라서 C, D를 처리하면 된다.
\[ 1 * (0.5) + 2 * (0.25) + 3 * (0.125) + 3 * (0.125) = 1.75 \]
2비트가 아니라 1.75 비트면 된다. 이렇게 절약된 비트는 자원의 절약을 뜻하기도 한다. 저장 공간을 떠올려도 좋고 통신이라면 오고 가는 전기 신호의 양으로 생각해도 좋겠다. 아래 두 개의 테이블을 비교해 보자. 계산의 편의를 위해서 로그의 밑수는 4로 잡았다.
| 정보 | \(p\) | \(\log_4 \frac{1}{p}\) | \(p \log_4 \frac{1}{p}\) | 비트 표현 | 비트수 |
|---|---|---|---|---|---|
| A | 0.25 | 1 | 0.25 | 00 |
2 |
| B | 0.25 | 1 | 0.25 | 01 |
2 |
| C | 0.25 | 1 | 0.25 | 10 |
2 |
| D | 0.25 | 1 | 0.25 | 11 |
2 |
| 정보 | \(p\) | \(\log_4 \frac{1}{p}\) | \(p \log_4 \frac{1}{p}\) | 비트 표현 | 비트수 |
|---|---|---|---|---|---|
| A | 0.5 | 0.5 | 0.25 | 1 |
1 |
| B | 0.25 | 1 | 0.25 | 01 |
2 |
| C | 0.125 | 1.5 | 0.1875 | 001 |
3 |
| D | 0.125 | 1.5 | 0.1875 | 000 |
3 |
위 두 표에서 보듯이, 첫 번째 정보 묶음의 섀넌 엔트로피는 1이다. 두 번째 묶음의 섀넌 엔트로피는 0.875다. 후자가 전자보다 작다. 이는 정보의 분포에 따라서 엔트로피가 가장 무질서한, 즉 가장 클 때보다 효율적인 인코딩 방법이 존재함을 보여준다.
Cross Entropy
크로스 엔트로피 역시 섀넌 엔트로피에서 파생된 개념이다. 크로스 엔트로피는 두 확률 분포의 차이를 측정하는 지표이다. 크로스 엔트로피는 다음과 같이 정의된다.
\[ H(p,q)=-\sum_{x \in \chi} p(x) \log q(x) \]
섀넌 엔트로피의 개념에서 확률의 효용을 측정하는 값으로 예측 확률을 사용한다고 보면 되겠다. 즉, 실제로 존재하는 확률이 \(p(x)\)라고 할 때 이를 예측한 값이 \(q(x)\)라고 하면, 위의 값은 실제 확률과 비교한 예측 확률의 성과를 나타난다. \(q(x) = p(x)\)일 때 \(H(p,q)\)는 최솟값을 지니게 된다.
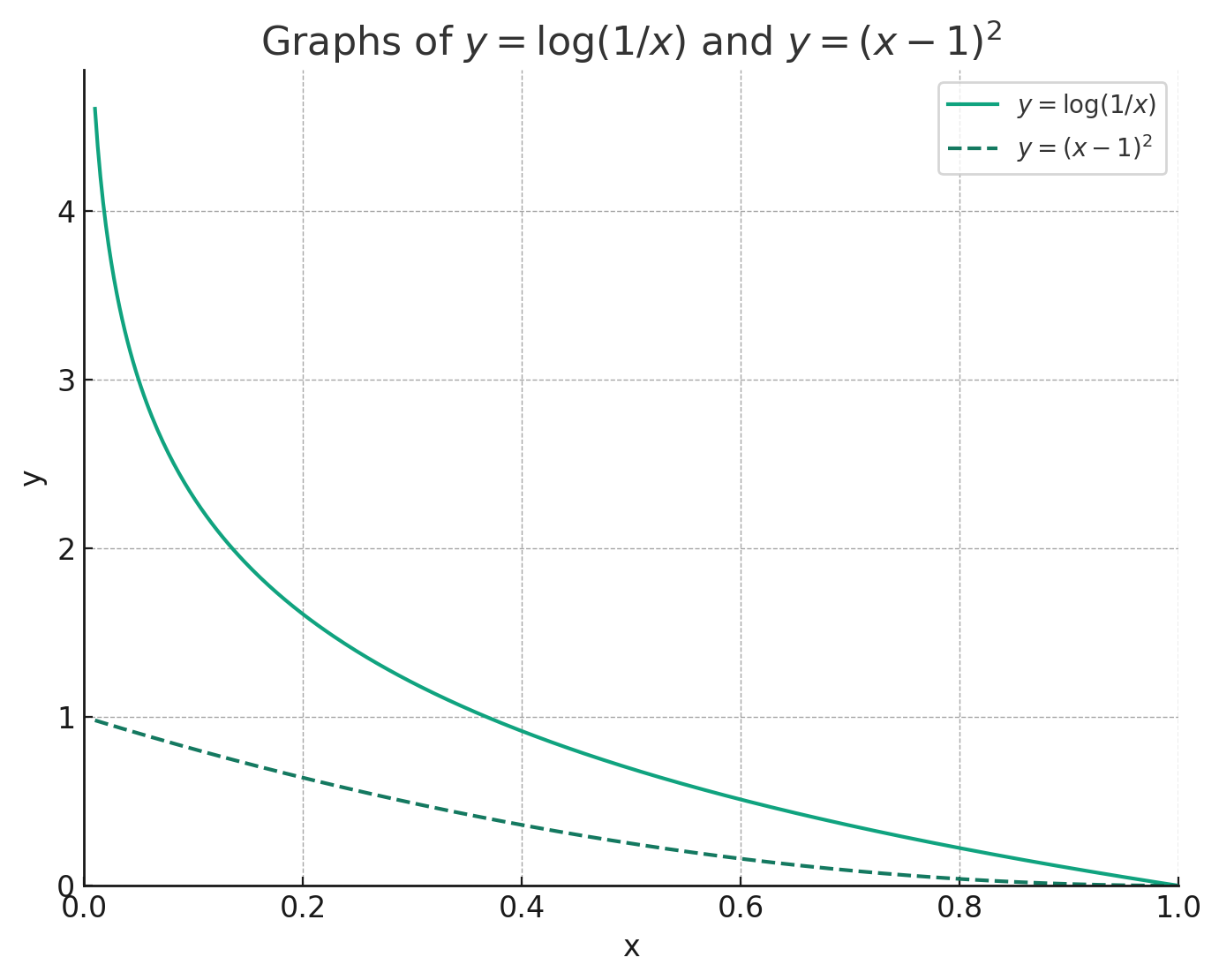
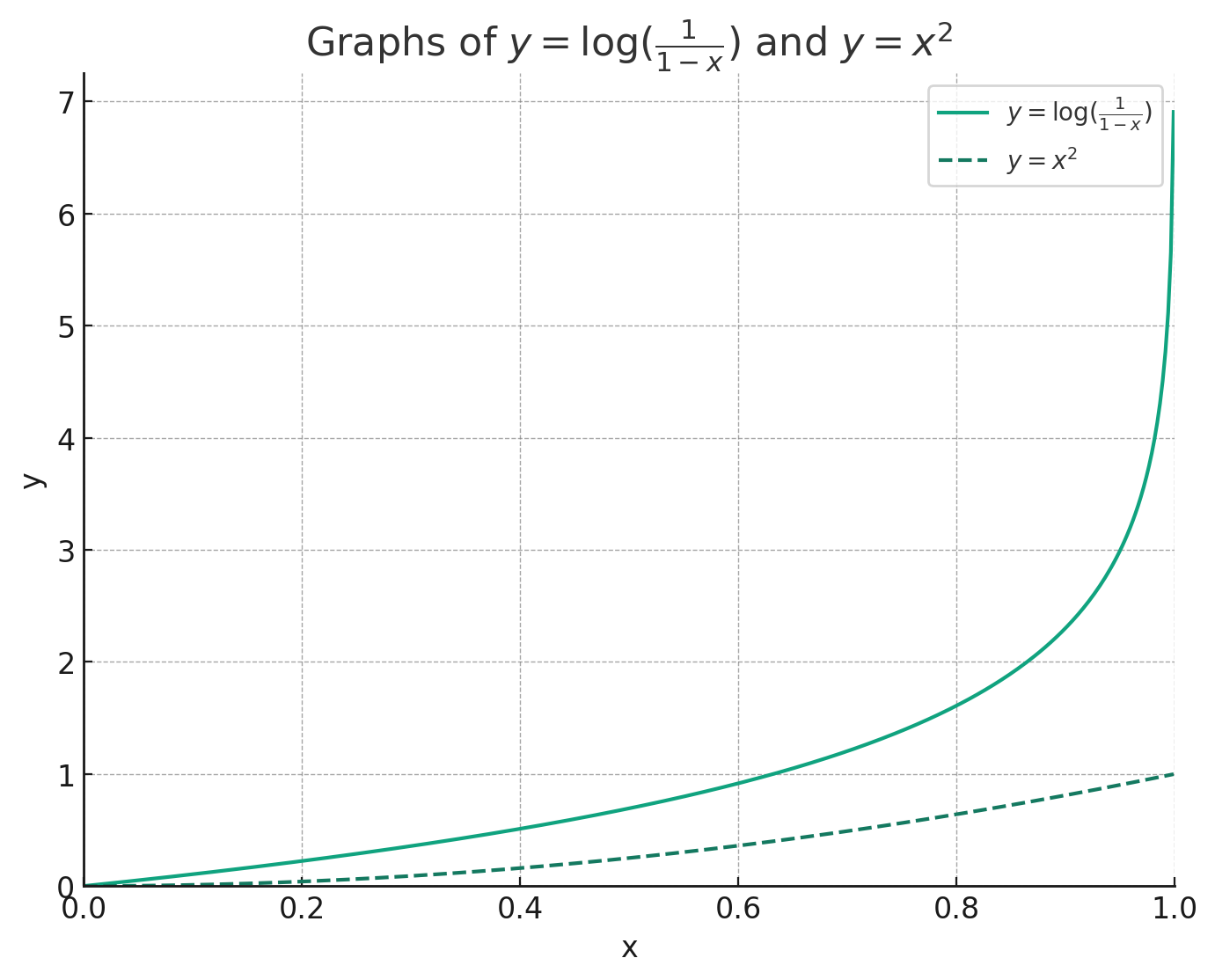
크로스 엔트로피는 분류 문제를 풀 때 손실 함수로 많이 활용된다. 왜 그럴까? 이것이 이른바 그래이언트 소실(vanishing gradient) 문제이다. 흔히 손실 함수로 활용되는 오차제곱항에 비해서 크로스 엔트로피 손실 함수는 올바른 확률에서 멀리 떨어져 있을 때 기울기의 값이 훨씬 크다. 이는 값이 \([0,1]\)에 다 위치하고 있기 때문이다. 경사 하강법을 쓸 때 크로스 엔트로피 오차 함수일 때 훨씬 빠르게 원하는 위치로 접근한다.
오차 함수로 크로스 엔트로피를 사용할 때의 그래디언트와 오차 함수로 평균 제곱 오차를 사용할 때의 그래디언트를 비교해보자. 왼쪽은 참 값이 1이고, 오른쪽은 참 값이 0이라고 가정했을 때의 그래디언트를 나타낸다.
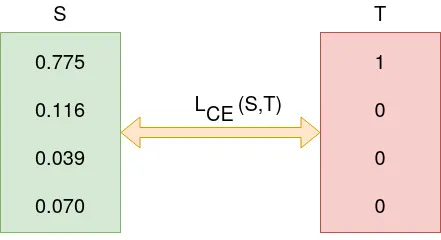
이산 분포를 가정했을 때 \(\chi\)를 전체 분류의 크기를 담은 첨수 집합이라고 하자. 이제 1이라는 종류만을 담은 참 값은 그림의 오른쪽과 같고, 반면 모델이 예측한 각 분류의 확률은 왼쪽이라고 하자. 이때 크로스 엔트로피는 아래 그림과 같이 계산될 수 있다. S는 \(q(x)\), T는 \(p(x)\)를 나타낸다.
기계학습에서 크로스 엔트로피와 관련된 내용은 statquest-cross entrophy를 참고하자.
로지스틱 함수의 경우
로지스틱 함수란 베르누이 분포(발생하거나 그렇지 않거나)를 지니는 사건의 확률을 표현하는 함수의 하나이다. 로지스틱 함수는 다음과 같이 정의된다.
\[ \sigma(x) = \frac{1}{1+e^{-x}} = \frac{e^x}{1+e^x} \]
로지스틱 함수가 편리한 이유는 \(x\)에 대해서 연속이고, \((0,1)\) 사이의 값이 매핑되기 때문에 확률값으로 근사해서 사용할 수 있다. 로지스틱 함수의 크로스 엔트로피를 구해보자.
\[ \begin{aligned} h(x) & = -p\log(\frac{e^x}{1+e^x}) - (1-p)\log(1-\frac{e^x}{1+e^x}) \\ & = \log(1+e^x) - px \end{aligned} \]
\(h'(x)\)의 값을 구하면 다음과 같다.
\[ h'(x) = \dfrac{e^x}{1+e^x} - p = \sigma(x) - p \]
앞서 언급한 대로 \(\sigma(x)-p = 0\)일 때 극대화 1계 조건이 완성된다. \(h''(x) > 0\)이므로 1계 조건이 만족할 때 최솟값을 \(H(x)\)는 최솟값을 지니게 된다. 즉, 로지스틱 함수가 측정하는 발생 확률이 실제의 \(p\)와 일치할 때 크로스 에트로피가 최솟값이 된다.