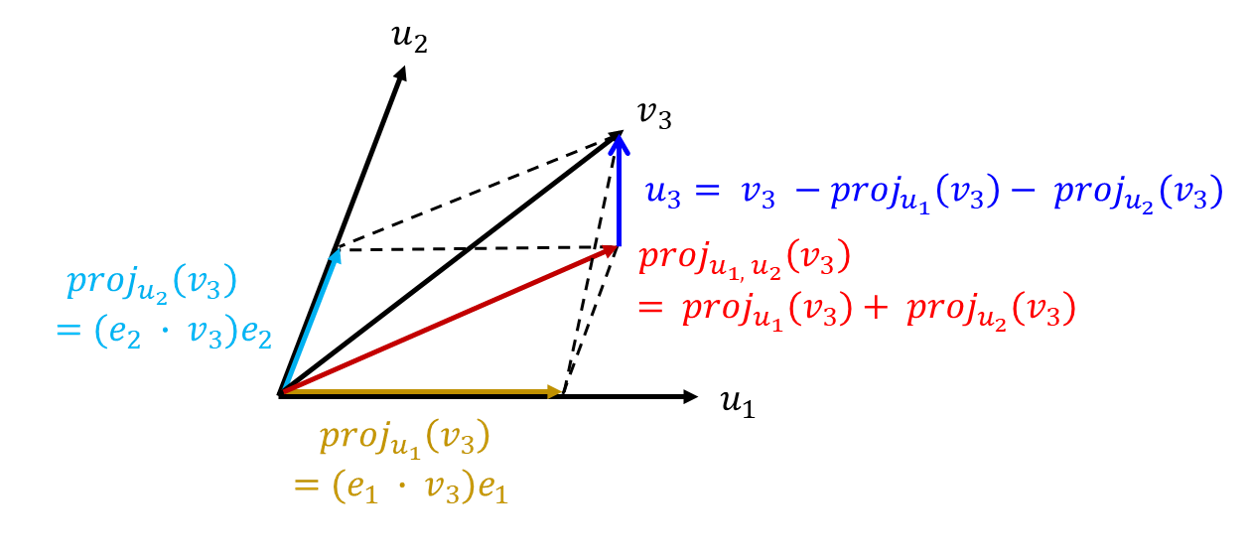Eigenspace, part 1
Why?
아이겐밸류, 아이겐벡터는 중요하다. 어디서나 튀어나온다. 그래서 친숙하지만 나는 이걸 제대로 알고 있는 것일까? 이번 포스팅에서는 아이겐 공간의 관점에서 이 문제를 살펴볼 예정이다.
사실 아이겐 공간은 \(n \times n\) 매트릭스의 숨은 구조(뼈대)와 같다. 아이겐밸류를 구하는 식을 떠올려보자.
\[ M_T \vec x = \lambda \vec x \]
\(M_T\)라는 \(n \times n\) 변환이 특정한 벡터 아래서는 스칼라 곱의 문제로 환원된다. 이런 의미에서 아이겐벡터는 \(M_T\)라는 매트릭스가 지닌 일종의 축이다. 이 축 위에서 변환이 다시 축으로 환원되기 때문이다. \(M_T\)의 원래 기저와 상관 없이, 이 아이겐벡터로 다시 기저를 구성한다고 생각해보자. 이때 아이겐밸류는 해당 축의 크기(길이)로 이해할 수 있다.
Eigenspace
아이겐 공간이란 무엇일까? 특정한 아이겐밸류 \(\lambda_i\)에 의해 파생되는 아이겐 공간은 다음과 같이 정의될 수 있다.
\[ E_{\lambda_i} \overset{\rm def}{=} \mathcal N (A - \lambda_i 1) = \{ \vec v | (A - \lambda_i ) \vec v = \vec 0 \} \]
즉, \(A - \lambda_i 1\)의 널 스페이스다. 사실 여기서 아이겐밸류를 구하는 공식도 파생된다. 아이겐벡터가 \(A - \lambda_i 1\)의 널 스페이스에 있다는 것은 \(A - \lambda_i 1\)라는 변환이 서로 선형 종속이라는 뜻이다. 즉 \(\det (A - \lambda_i 1) = 0\)의 의미와 같다. 아이겐밸류를 구하는 특성방정식이 여기서 도출된다.
\[ p(\lambda) = \vert A - \lambda 1 \vert = 0 \]
All distinct eigenvalues
실용적으로 접근해보자. 모든 아이겐밸류가 다르다면, 아이겐벡터는 선형독립이다. \(n\) 개의 서로 다른 아이겐벡터가 있다면 원래 매트릭스(\(M_T\))의 컬럼 스페이스를 생성하는 기저가 될 수 있다.
Algebraic vs geometric
대수적 중복도(algebraic multiplicity: AM)란 특성 방정식에서 특정한 아이겐밸류 \(\lambda\)가 몇 번 나타나는지를 표시한다. 한편 기하적 중복도(geometric multiplicity: GM)란 \(\lambda\)의 아이겐벡터가 생성하는 널 공간의 차원을 의미한다. 예를 들어보자.
\[ A = \begin{bmatrix} 1 & 2 \\ 0 & 1 \end{bmatrix} \]
\(A\) 특성방정식을 구하면 \(p(\lambda) = (1-\lambda)^2\)이다. 따라서 아이겐밸류 1의 AM는 2이다. GM은 어떨까?
\[ A - \lambda I = \begin{bmatrix} 0 & 2 \\ 0 & 0 \\ \end{bmatrix} x = 0 \]
이를 만족하는 널 스페이스 \(x\)는 아래 벡터 하나다.
\[ x = \alpha \begin{bmatrix} 1 \\ 0 \end{bmatrix} \]
따라서 \(\lambda=1\)의 GM은 1이 된다.
일단 직관적으로 알 수 있는 점은 아이겐밸류 \(\lambda\)의 기하적 중복도가 대수적 중복도 보다 클 수는 없다는 점이다. 즉, \({\rm GM}(\lambda) \leq {\rm AM}(\lambda)\)
Defective eigenvalues
\({\rm GM}(\lambda) < {\rm AM}(\lambda)\)가 되는 \(\lambda\)를 defective eigenvalue라고 부른다. 특성 방정식에서 해당 아이겐벡터가 생성하는 널 스페이스의 차원이 AM보다 작다면, 아이겐벡터를 모아서 특성 방정식 생성한 널 스페이스를 생성할 수 없다. 다시 말하면, 이는 아이겐 분해를 통해서 원래 매트릭스의 컬럼 스페이스를 온전하게 생성할 수 없다는 뜻이다.
모든 아이겐밸류의 값이 다를 경우, 즉 아이겐밸류의 중복이 없을 경우 각각 아이겐밸류의 AM은 1이 된다. 이 경우 아이겐벡터들이 모두 선형 독립이기 때문에 각 아이겐밸류의 기하적 중복도 역시 1이 된다. 따라서 반복되는 아이겐밸류가 없는 경우에는 defective eigenvalue는 없고, 행렬의 아이겐 분해가 가능해진다.
Diagonalization as Change-of-Basis
아이겐벡터와 아이겐밸류를 동원해서 매트릭스를 분해하는 것을 대각화라고도 부른다.
\[ A = Q \Lambda Q^{-1} \]
이렇게 분해될 때 가운데 매트릭스 \(\Lambda\)가 아이겐밸류의 대각 행렬로 구성되기 때문이다. \(Q\)는 다음과 같이 정의된다.
\[ Q = \begin{bmatrix} \vert & \vert & \vert \\ \vec e_{\lambda_1} & \dotsc & \vec e_{\lambda_n} \\ \vert & \vert & \vert \\ \end{bmatrix} \]
앞서 아이겐벡터가 일종의 축의 역할을 한다고 했다. 즉, 이 아이겐벡터는 매트릭스의 인풋으로 아이겐 스페이스 벡터를 받고 이를 현재의 표준 스페이스로 바꿔준다.\(B_S \leftarrow B_\lambda\) 역할을 한다. 즉,
\[ Q = \phantom{}_{B_S}[1]_{B_\lambda} \]
\(Q\)를 기저 변환의 관점에서 보면 아이겐 공간의 좌표를 표준 좌표로 바뀌주는 역할을 한다. \(Q^{-1}\)은 반대로 \(B_{\lambda} \leftarrow B_{S}\)의 역할을 한다. 즉,
\[ Q^{-1} = \phantom{}_{B_\lambda}[1]_{B_S} \]
이 관점에서 보면 행렬의 대각화가 새롭게 보인다.
\[ [\vec w]_{B_S} = \phantom{}_{B_S}[A]_{B_S} [\vec v]_{B_S} = Q \Lambda Q^{-1}[\vec v]_{B_S} \]
\[ Q \Lambda Q^{-1}[\vec v]_{B_S} = \underbrace{\phantom{}_{B_S}[1]_{B_\lambda}}_{Q}\phantom{}_{B_\lambda}[\Lambda]_{B_\lambda}\overbrace{\phantom{}_{B_\lambda}[1]_{B_S}}^{Q^{-1}}[\vec v]_{B_S} \]
행렬의 대각화란 일정한 변환 혹은 매트릭스를 아이겐 공간을 통해 다시 해석하는 과정이다. 즉, \(B_S \to B_\lambda \to B_S\)의 과정을 거친다.
대각 행렬 \(\Lambda\)는 아이겐벡터들로 구성된 아이겐 공간의 기저(아이겐벡터)의 크기를 나타낸다.
외우자!
대각화를 통해서 아이겐밸류의 중요한 특성 두 가지를 다시 음미해보자.
\[ {\rm det}(A) = \vert A \vert = \prod_{i} \lambda_i \]
\[ {\rm Tr}(A) = \sum_{i} a_{ii} = \sum_{i} \lambda_i \]
논리는 아래와 같이 간단하다.
\[ \vert A \vert = \vert Q \Lambda Q^{-1} \vert = \vert Q \vert \vert \Lambda \vert \vert Q^{-1} \vert = \vert Q \vert \vert Q^{-1} \vert \vert \Lambda \vert = \dfrac{\vert Q \vert}{\vert Q^{} \vert} \vert \Lambda \vert = \vert \Lambda \vert \]
\[ {\rm Tr}(Q \Lambda Q^{-1}) = {\rm Tr}(\Lambda Q Q^{-1}) = {\rm Tr}(\Lambda 1) = {\rm Tr}(\Lambda) = \sum_{i} \lambda_i \]
두 가지 속성은 \({\rm det}(A) = \vert A \vert = \prod_{i} \lambda_i\)는 대각화가 가능한 경우 뿐 아니라 일반적으로 성립한다. 첫번째 속성만 살펴보자. 특성방정식을 생각해보면, \(\vert A - \lambda I \vert = 0\)이다. 즉,
\[ \begin{aligned} p(\lambda) = & {\rm det} (A - \lambda I) \\ & (-1)^n (\lambda - \lambda_1) \dotsb (\lambda - \lambda_n) \\ & (\lambda_1 - \lambda)\dotsb(\lambda_n - \lambda) \end{aligned} \]
따라서, \(\det (A) = \lambda_1 \dotsb \lambda_n\).
Normal matrix
매트릭스 \(A\)가 노멀이라면, 이는 \(A^T A = A A^T\)를 만족하는 경우를 뜻한다. 모든 노멀 매트릭스는 대각화가 가능하고 아울러 \(Q\)를 직교 행렬(orthgonal matrix or orthonormal matrix) \(O\) 로 택할 수 있다. 이는 \(Q^{-1}\)의 계산이 간단해진다는 뜻이다. 즉,
\[ OO^T = I = O^T O \]
\[ O^TO = \begin{bmatrix} -- & \hat e_1 & -- \\ & \vdots & \\ -- & \hat e_n & -- \\ \end{bmatrix} \begin{bmatrix} \vert & & \vert \\ \hat e_1 & \dotsc & \hat e_n \\ \vert & & \vert \\ \end{bmatrix} = I \]
Gram-Schmidt Orthogonalization
orthnormal, orthogonal, generic 세 가지 기저의 품질을 따져보자. 당연히 orthonormal 기저가 가장 작업하기 쉽다. 위에서 보듯이, \(Q^T = Q^{-1}\)라는 좋은 특징도 지니고 있다. 만일 통상적인 벡터를 orthonormal 기저로 변형할 수 있다면, 작업이 훨씬 쉬울 것이다.
Definition
- \(V\): \(n\) 차원 벡터
- \(\{ v_1, \dotsc, v_n \}\): \(V\)의 generic 기저
- \(\{ e_1, \dotsc, e_n \}\): \(V\)의 orthogonal 기저. \(e_i \cdot e_j = 0\) for \(i \neq j\)
- \(\{\hat e_1, \dotsc, \hat e_n \}\) V의 orthonormal 기저.
- Inner production operation: \(\langle \cdot, \cdot \rangle: V \times V \to \mathbb R\)
- Length: \(\Vert v \Vert = \langle v, v \rangle\)
- Projection operation: Projection of \(u\) onto \(e\):
\[ \Pi_e(u) = \dfrac{\langle u, e \rangle}{\Vert e \Vert^2}e \]
- The projection complement of projection \(\Pi_e(u)\) is \(w\)
\[ \Pi_e(u) + w = u ~~~\Rightarrow~~~w = u - \Pi_e(u) \]
Orthonormal basis is nice
어떤 벡터 \(v\)든 orthonormal 기저를 통해 간편하게 나타낼 수 있다. 즉,
\[ v = \langle v, \hat e_1 \rangle \hat e_1 + \dotsb + \langle v, \hat e_n \rangle \hat e_n \]
Orthogonalization
일단 기억해야 할 것은 generic 기저 \(\{v_i\}\)가 생성하는 벡터 공간과 \(\{ \hat e_i \}\)가 생성하는 벡터 공간이 동일하다는 것이다. 즉,
\[ \text{span}(v_1, \dotsc, v_n) = V = \text{span}(\hat e_1, \dotsc, \hat e_n) \]
그람-슈미트 알고리즘은 다음과 같다.
- 일단 orthogonal 기저를 만든다.
- 해당 벡터를 표준화한다.
Orthogonal 기저는 어떻게 만들까? 먼저 과정을 살펴보자. .
- \(e_1 = v_1\)
- \(e_2 = v_2 - \Pi_{e_1}(v_2)\)
위의 그림에서 보듯이 \(v_2\)는 \(v_1\) 프로젝션된 벡터와 이와 직교하는 \(e_2\)와의 합으로 계산할 수 있다. 따라서 \(e_2 = v_2 - \Pi_{e_1}(v_2)\)가 성립한다. 벡터의 빼기 관점에서 생각해보면 어떨까? \(v_2\)와 \(\Pi_{e_1}(v_2)\)의 차이가 \(e_2\)다. 벡터는 방향과 크기로 정의된다는 점을 다시 기억하자. 같은 방식으로 아래 그림에서 보듯이 더 많은 축과 직교하는 벡터들을 구성할 수 있다.
이후 \(\hat e_i = \dfrac{e_i}{\Vert e_i \Vert}\)로 \(e_i\)를 표준화하면 된다.
\[ v = {\rm proj}_{u_1} (v) + {\rm proj}_{u_2}(v) + w \]
즉, 원래 벡터(\(v\))에서 이미 확립된 직교 벡터에서 \(v\)로 쏜 프로젝션 벡터를 빼주면 원하는 새로운 직교 벡터를 얻을 수 있다. 따라서
\[ \begin{aligned} e_3 & = v_3 - \Pi_{e_1}(v_3) - \Pi_{e_2}(v_3) \\ &~~~\vdots \\ e_n & = v_n - \sum_{i=1}^{n-1} \Pi_{e_i}(v_n) \end{aligned} \]
Wrap-it-up
행렬 대각화에 관해서 다시 한번 정리해보자. 때로는 혼동될 사안이라서 정리한다. 증명은 일단 생략한다.
Diagonalization Theorem
매트릭스 \(A \in \mathbb C^{n \times n}\)가 대각화가 가능하다는 것은 \(n\)의 선형 독립인 아이겐벡터를 지니고 있다는 뜻이다. 즉, \(A =Q \Lambda Q^{-1}\) 형태로 분해될 수 있음을 뜻한다.
- 착각하지 말아야 할 것! 대각가능 행렬과 역행렬이 존재하는 행렬은 아무 관계가 없다. 둘은 서로 다른 이야기다.
- 아이겐분해(eigendecomposition)이란 닮음 행렬을 통해서 기저를 바꾸는 과정인데, 이때 기저를 바꾸는 매트릭스로 동원되는 것이 아이겐벡터 매트릭스다.
외우자!
- \(A\) positive semidefinite \(\Rightarrow\) 아이겐밸류는 비음이다.
- \(A\) symmetric \(\Rightarrow\) 아이겐밸류는 실수
- \(A\) normal (\(A^T A = A A^T\)) \(\Rightarrow\) \(Q\)를 직교 행렬 \(O\)로 고를 수 있다(\(O^T O = I\)).