Vector Geometrically, part 1
tl; dr
- 벡터와 포인트를 오가는 방법을 배우자.
Concepts
편의상 3차원 공간으로 예시하도록 한다. \(n\) 차원으로 확장은 쉽게 된다.
- \(p = (p_x, p_y, p_z)\): \(p \in \mathbb R^3\) is a point
- \(\vec v = (v_x, v_y, v_z)\): \(\vec v \in \mathbb R^3\) is a vector
- \(\hat v = \frac{v}{\lVert v \lVert}\): Unit vector
First thing first
점과 벡터의 차이를 다시 새기고 가자.
- 점은 공간에서 위치를 지니고 있다. 점의 특성은 위치 뿐이다.
- 벡터는 크기와 방향을 지니고 있다. 벡터는 공간에서 위치를 지니고 있지 않다.
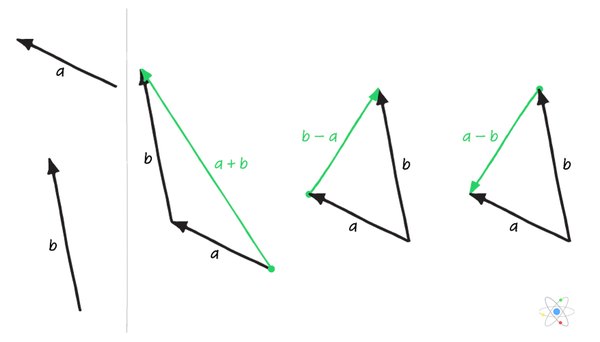
?@fig-vector/a에서 보듯이 벡터 \(a\)와 벡터 \(b\)는 크기와 방향성만 지니고 있을 뿐이다.
Vector
좌표에서 점과 점을 연결하면 이를 통해 벡터를 얻을 수 있다. \(P_0\)를 지나는 무한의 1차원 벡터는 다음과 같이 정의된다.
- Parametric equation:
\[ l : \lbrace p_0 + t \vec v, t \in \mathbb R \rbrace \]
위의 그림을 보면서 식을 도출해보자. 포인트 \(P_0\)를 (원점 기준) 벡터로 나타내면 \(\vec r_0\)가 된다. 그리고 \(P\) 점을 벡터로 나타내면 \(\vec r\)이 된다. 벡터 \(\overrightarrow{P_0\, P}\)와 수평인 벡터를 \(\vec v\)라고 하자. 이 두 가지 사실을 조합하면 다음과 같다.
- \(\overrightarrow{P_0 \, P} = \overrightarrow{O \, P} - \overrightarrow{O \, P_0} = \vec r - \vec r_0\)
- \(\vec r - \vec r_0 = t v\)
위 결과에 따라서 파라메트릭 식이 도출된다.
- Cartesian(symetric) equation:
\[ l: \lbrace \dfrac{x - p_{0x}}{v_x} = \dfrac{y - p_{0y}}{v_y} = \dfrac{z - p_{0z}}{v_z} \rbrace \]
\(p_{ab}\)에서 \(a\)는 해당 점의 인덱스이며, \(b\)는 해당 점의 개별 좌표를 나타낸다. 즉, \(b \in \{ x, y, z \}\)이다.
도출 과정은 아래와 같다. 앞서 파리메트릭 표현에서 임의 \(P\)의 좌표 \((x, y, z)\)는 다음과 같다.
\[ \vec r = (x, y, z) = ( p_{0x} + t v_x, p_{0y} + t v_y, p_{0z} + t v_z ) \]
\[ \dfrac{x - p_{0x}}{v_x} = \dfrac{x - p_{0y}}{v_y} = \dfrac{x - p_{0z}}{v_z} = t \]
Plane
\(p_0\)를 지나는 무한 평면 P는 다음과 같이 정의된다. 평면을 평면을 표현하기 위해서는 벡터 두 개( \(\vec v, \vec w\) )가 필요하다. 먼저 평면을 표현하는 가장 일반적인 방정식을 살펴보자.
- General equation: \(P: \lbrace Ax + By + Cz = D \rbrace\)
이를 파라메트릭 식으로 표현하면 아래왁 같다.
- Parametric equation: \(P : \lbrace p_0 + s \vec v + t \vec w~\text{where}~s,t \in \mathbb R \rbrace\)
마지막으로 기하학적으로 표현하는 방법은 아래와 같이 노멀 벡터를 활용하는 것이다.
- Geometric equation: \(P : \lbrace (x, y, z) \in \mathbb R^3 | \vec n \cdot [(x,y,z) - p_0] = 0 \rbrace \text{~with normal vector $\vec n$}\)
More on normal vector
노멀 벡터는 아래 평면(plane) 혹은 벡터과 직교하는 성분의 벡터다. 이 녀석을 어떻게 구할까? 평면 \(P\)의 parametric 식을 보자. 2차원 플레인을 구성하는 두 벡터 \(\vec v\), \(\vec w\)가 있다. 노멀 벡터는 이 두 성분 모두와 직교하는 성분의 벡터이다. 이는 바로 크로스 프로덕트의 정의이다.
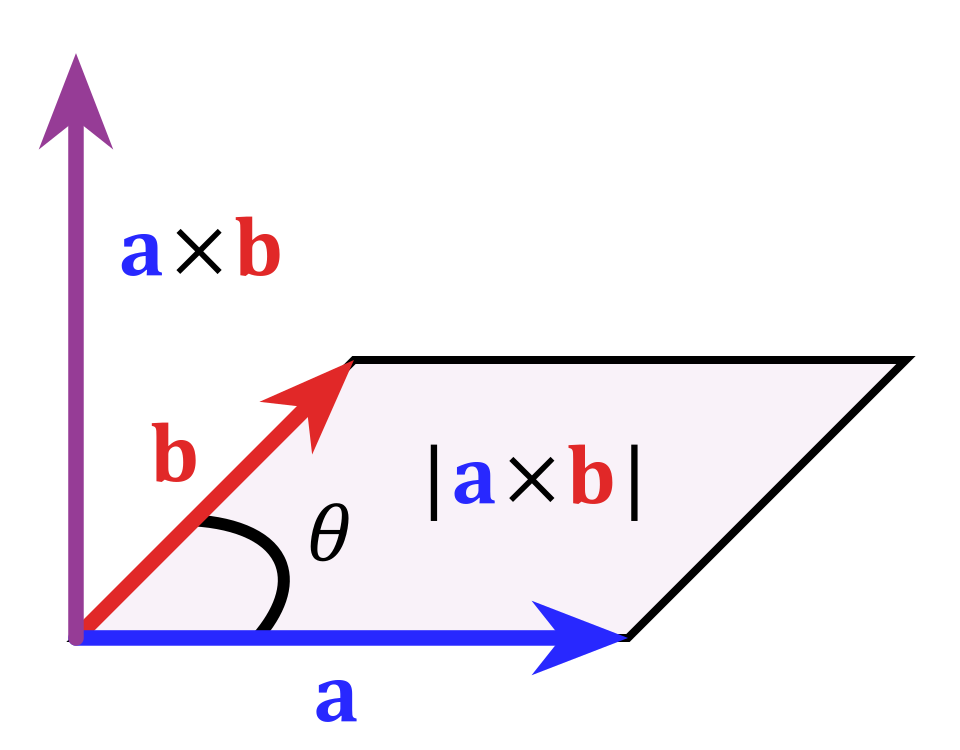
크로스 프로덕트는 두 벡터와 직교하면서 두 벡터가 생성하는 면적이 길이가 되는 벡터를 생성한다. 닷 프로덕트가 스칼라 값을 생성하는 것과 다르다는 점에 주의하자. 위키를 참고하자.
평면위의 어떤 세 점 \(p, q, r\)이 있다고 하자. 평면 위에 존재하는 벡터 두 개를 \(\vec v = q - p\), \(\vec w = r - p\)과 같이 만들자. 이 벡터와 직교하는 벡터 \(\vec n\) 중 가장 편리하게 찾을 수 있는 것은 \(\vec v\),\(\vec w\)의 크로스 프로덕트와 같다.
\[ \vec n = \vec v \times \vec w = (q-p) \times (r-p) \]
Distance
거리 역시 세 가지로 나누어 이해해보자. 점과 점 사이의 유클리드 거리는 생략하겠다. 벡터와 점의 거리는 어떻게 구할까? 플레인과 점의 거리는 어떻게 구할까? 이 포스팅을 참고하라.