Eigenvalues and Eigenvectors

고유치와 고유벡터에 관해 알아보자.

TL; DR

• 행렬 대각화를 이루는 방법 중 하나는 아이겐벡터와 아이겐밸류를 재구성하는 것이다.
• 대각화가 가능한 행렬 \(A\)가 있고, 그 아이겐벡터를 열 벡터로 하는 행렬을 \(Q\)라고 하면

\[ \begin{aligned} A Q & = A[x_1, \dotsc, x_n] \\ & = [\lambda_1 x_1, \cdots, \lambda_n x_n] \\ &= Q \boldsymbol{\lambda} \end{aligned} \]

\[ AQ Q^{-1} = A = Q \boldsymbol{\lambda}Q^{-1} \]

• 대각화가 가능하기 위해서는 우선 행렬 \(Q\)가 비특이(non-singular) 행렬이어야 한다. \(Q\)는 아이겐벡터의 조합이기 때문에 서로 다른 아이겐밸류를 지니거나 혹은 아이겐벡터의 선형독립이 성립해야 한다.
• 대칭 행렬의 경우 모든 아이겐밸류가 실수이고, \(Q\)는 직교 행렬(orthogonal matrix)이 된다. 이 경우

\[ A = Q\boldsymbol{\lambda}Q^T \]

Definition

\[ \underset{(n \times n)}{\boldsymbol{A}} \underset{(n \times 1)}{x} = \lambda x, \text{ for $x \neq 0$} \]

고유치와 고유벡터는 영어 단어 발음 그대로 아이겐밸류와 아이겐벡터로로 쓰기로 하자.

벡터 \(x(\in {\mathbb R}^n)\)가 있다고 하자. \(\boldsymbol{A}\)는 일종의 함수이고 이는 \(x\)를 변형시키게 된다. 이 변형이 그 다시 자신이 되고 벡터의 크기만 조정해주는 형태가 될 때, \(\lambda\)를 아이겐밸류 그리고 그 벡터 \(x\)를 아이겐벡터라고 한다. 잠깐! 여기서 아이겐 벡터는 우 아이겐벡터다. 왜냐하면, 벡터가 매트릭스의 오른쪽에 곱해지기 때문이다. 우(right) 아이겐벡터를 보통 아이겐벡터라고 쓴다. 하지만 좌(left) 아이겐벡터도 있다. 일단 이 점만 지적해두도록 하자.

좌 아이겐벡터와 우 아이겐벡터가 절묘하게 사용되는 사례는 마르코프 체인이다. 아이겐밸류 1이 존재하고, 그 아이겐벡터가 해당 상태의 극한 분포가 된다는 사실이 좌, 우 아이겐벡터를 번갈아 사용하면서 도출된다. 자세한 것은 여기를 참고하자.

Eigenspace

벡터들의 집합 중에서 아래의 조건을 만족하면 이를 벡터 (부분) 공간이라고 부른다.

1. 영 벡터 \(\boldsymbol 0\)가 원소이다.
2. \(x\)가 원소일 때 \(\alpha x\) (\(\alpha \in \mathbb{R})\)도 원소다. \(\alpha \in \mathbb R\)
3. \(x\), \(y\)가 원소일 때 \(x + y\)도 원소다.

쉽게 말해서 벡터 (부분) 공간 위에서 덧셈과 스칼라 곱셈이 정의되고, 0 벡터가 포함되어 있으면 벡터 공간이 구성된다. 그렇다면 아이겐벡터 공간을 정의해보자. 우선, 같은 아이겐밸류 \(\lambda\)에 대해서 다음과 같은 벡터 공간이 정의되면 된다.

1. \(A {\boldsymbol 0} = \lambda {\boldsymbol 0}\)
2. \(A(\alpha x) = \alpha(A x) = \alpha (\lambda x) = \lambda(\alpha x)\)
3. \(A(x_1 + x_2) = A x_1 + A x_2 = \lambda x_1 + \lambda x_2 = \lambda(x_1 + x_2)\)

3번의 경우 정의대로 하나의 아이겐밸류 \(\lambda\)에 대해서 두 개 이상의 아이겐벡터가 대응될 때에 해당한다. 아이겐벡터를 원소로 하는 공간은 벡터 부분 공간이 되며, 이를 아이겐스페이스(eigenspace)라고 부른다. 정리하면, 같은 아이겐밸류를 공유한다면, 아이겐벡터의 어떤 선형 결합도 해당 아이겐밸류의 아이겐벡터가 된다.

얼핏 생각하면 이런 경우가 있나 싶을 수 있다. 가장 좋은 사례는 항등 행렬, \({\boldsymbol I}_n\)이다. 이 항등행렬의 경우 아이겐밸류는 1이고, 대응 가능한 어떤 벡터도 아이겐벡터가 된다.

Determinant and Eigenvalues

아이겐밸류의 아이겐벡터를 구하는 과정은 다음과 같다.

\[ |(\boldsymbol{A} - \lambda I)| = 0 \]

즉, 임의의 아이겐밸류, 아이겐벡터 정의에서 \(\boldsymbol 0\) 벡터가 아닌 \(x\)를 \(\boldsymbol 0\) 벡터로 만들기 위해서는 위의 행렬식 값이 0이어야 한다. 즉 \((\boldsymbol{A} - \lambda I)\)이 선형 종속이어야 한다. 이때 행렬식이 \(\lambda\)의 \(n\) 차 방정식이고, \(n\)차 방정식의 근이 각각 아이겐밸류가 된다. 즉,

\[ |(\boldsymbol{A} - \lambda {\boldsymbol I})| = (\lambda_1 - \lambda) \cdot (\lambda_2 - \lambda) \dotsb (\lambda_n - \lambda) \]

위의 식에서 두가지 사실을 알 수 있다.

1. \(\boldsymbol{A}\)의 행렬식은 아이겐밸류의 곱과 같다. 즉, \(\lambda = 0\)을 넣으면 이 결과를 쉽게 얻을 수 있다.
2. 가역행렬(invertible matrix)이 될 조건, 즉 역행렬이 존재할 조건은 행렬식의 값이 0이 아닌 경우다. 1에 따르면 이는 모든 아이겐밸류의 값이 0이 아닌 조건과 동치다.

Transpose

원래 행렬의 행렬식과 전치행렬의 행렬식은 같다. 이를 아이겐밸류 계산에 응용해보자.

\[ |\boldsymbol{A}^T - \lambda {\boldsymbol I}| = |(\boldsymbol{A}-\lambda {\boldsymbol I})^T| = |\boldsymbol{A}-\lambda {\boldsymbol I}| \]

즉, 원래 행렬 \(\boldsymbol{A}\)와 전치 행렬 \(\boldsymbol{A}^T\)는 같은 아이겐밸류를 갖는다.

Diagonalization

아이겐밸류와 아이겐벡터가 가장 많이 사용되는 경우는 행렬의 대각화이다. 여기서 대각화란, 정방 행렬의 대각에 위치한 원소, \(a_{ii}\)를 제외한 나머지 원소가 모두 0인 행렬, 즉 대각 행렬을 품는 변형을 의미한다. 대각 행렬은 여러가지로 쓸모가 많다. 특히 행렬의 \(k\) 제곱이 필요한 경우 대각행렬은 그냥 해당 대각원소의 \(k\) 제곱과 동일해진다. 행렬의 대각화를 살펴보자.

\[ y = \boldsymbol{A} x \]

기본적으로 행렬은 함수다. 즉, 벡터 \(x\)를 투입(input)으로 보면 이를 선형 결합을 통해서 다른 어떤 산출(output) 벡터로 보내는 것이다. 일단 설명의 편의를 위해서 \(x\)가 2차원 벡터라고 두고 설명해보자. 즉,

\[x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}. \]

\(\boldsymbol{A}\)에 의해 변형된 결과를 아이겐벡터 \(v_1\)과 \(v_2\)를 통해서 표현할 수 있다고 가정하자. \(v_1\), \(v_2\)를 통해 \(x\), \(y\)를 표현하면 다음과 같다.

\[ \begin{aligned} x & = w_1 v_1 + w_2 v_2 \\ y & = z_1 v_1 + z_2 v_2 \end{aligned} \]

이때, \(w_\cdot\), \(z_\cdot\)은 스칼라 값임에 유의하자. 이를 매트릭스로 표시하면 다음과 같다.

\[ x = \boldsymbol{Q} \begin{bmatrix} w_1 \\ w_2 \end{bmatrix},~ y = \boldsymbol{Q} \begin{bmatrix} z_1 \\ z_2 \end{bmatrix}, \text{where} \]

\[ \boldsymbol{Q} = \begin{bmatrix} v_1, v_2 \end{bmatrix} \]

\(v_i' v_i = 1(i = 1,2)\) 이고, \(v_1 \cdot v_2 = 0\) 이라고 가정하자. 즉, \(Q\)가 직교행렬이라고 가정하자.

\[ \begin{aligned} \boldsymbol{Q}z & = \boldsymbol{A} \boldsymbol{Q} w \\ z & = \boldsymbol{Q}^{-1} \boldsymbol{A} \boldsymbol{Q} w \\ z & = \boldsymbol{Q}^T \boldsymbol{A} \boldsymbol{Q} w \end{aligned} \]

직교행렬의 경우 \(\boldsymbol{Q}^{-1} = \boldsymbol{Q}^T\)가 성립한다. 이때

직교행렬의 경우 \(\boldsymbol{Q}^T \boldsymbol{Q} = \boldsymbol{Q} \boldsymbol{Q}^T = {\boldsymbol I}\)가 성립한다. 따라서 \(\boldsymbol{Q}^{-1} = \boldsymbol{Q}^T\)

\[ \boldsymbol{A} \boldsymbol{Q} = [A v_1, A v_2] = [\lambda_1 v_1, \lambda_2 v_2] = [v_1, v_2] \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} = \boldsymbol{Q} \boldsymbol{\lambda}. \]

따라서,

\[ z = \boldsymbol{Q}^T \boldsymbol{Q} \boldsymbol{\lambda} w \]

여기서 대각화의 핵심은

\[ \boldsymbol{Q}^T \boldsymbol{A} \boldsymbol{Q} = \boldsymbol{\lambda}\text{ or }\boldsymbol{A} = \boldsymbol{Q}\boldsymbol{\lambda}\boldsymbol{Q}^T \]

즉, 어떤 매트릭스의 아이겐벡터가 서로 직교하면 이를 통해 직교행렬 \(\boldsymbol{Q}\)를 얻을 수 있다. 이를 원래 매트릭스의 좌우로 곱하면 아이겐밸류를 대각원소로 갖는 대각행렬을 얻을 수 있다.

Generalization

일반화 해보자. 대각화는 다음과 같다.

\[ \boldsymbol{AQ} = \boldsymbol{A} [x_1, \dotsc, x_n] = [\lambda_1 x_1, \dotsc, \lambda_n x_n] = [x_1, \dotsc, x_n] \begin{bmatrix} \lambda_1& \dotsc & 0 \\ \vdots& \ddots& \vdots \\ 0& \dotsc& \lambda_n \end{bmatrix} = \boldsymbol{Q} \boldsymbol{\lambda} \]

행렬의 분해(factorization)은 다음을 의미한다.

\[ \boldsymbol{A} = \boldsymbol{Q} \boldsymbol{\lambda} \boldsymbol{Q}^{-1} \]

Diagonalizable

쉽게 생각하자. 우선 \(Q^{-1}\)이 존재해야 한다. 즉, \(Q\)가 비특이 행렬이어야 한다. \(Q\)가 비특이 행렬이 되기 위한 조건들은 일단 행렬 대각화를 위한 필요 조건이다.

그런데 \(Q\)는 아이겐벡터들로 구성된 행렬이다. 따라서 \(Q\)가 비특이 행렬이 되기 위해서는 해당 아이겐밸류들이 모두 다르거나, 중복된 아이겐밸류가 있다면 아이겐벡터의 선형 독립이 성립해야 한다. 아이겐밸류가 모두 다르면, 즉 각기 다른 아이겐백터가 존재하면, 대각화가 가능하다. 만일 아이겐밸류가 중복이라면, 경우에 따라서 다르다.

아이겐밸류가 중복인데 아이겐벡터가 서로 다를 수 있을까? 가장 좋은 예는 단위행렬이다. \(\mathbf I_n\)은 1의 아이겐 밸류만을 지니며 모든 벡터 \(x\)가 아이겐벡터가 된다.

Symmetric matrix

행렬이 대칭일 경우 \(Q\)는 다루기 편리한 특성을 더 지니게 된다.

1. \(\boldsymbol A\) 의 아이겐밸류는 모두 실수이다.
2. \(Q\)는 직교행렬이다. 즉, \(Q^T = Q^{-1}\) 가 성립한다.

이를 종합하면 아래와 같다.

\[ \boldsymbol{A} = \boldsymbol{Q} \boldsymbol{\lambda} \boldsymbol{Q}^{-1} = \boldsymbol{Q} \boldsymbol{\lambda} \boldsymbol{Q}^{T} \]

이런 작업이 왜 필요할까? 계산에 관점에서 접근하면 쉽게 이해할 수 있다. 사람이 하든 컴퓨터가 하든 매트릭스의 곱이나 역행렬을 구하는 과정에는 자원이 소모된다. 만일 매트릭스의 크기가 크다면 더욱 그럴 것이다. 그런데, A를 대각화할 수 있고 A가 선형이면 이 과정이 매우 편리해진다. \(\boldsymbol{Q}\)와 \(\boldsymbol{Q}^{T}\)를 구하고 아이겐밸류의 승수를 알고 있으면 매트릭스의 곱을 쉽게 구할 수 있다.

Graphic interpretation with vector space

앞서의 식을 다시 음미해보자.

\[ AQ = A[x_1, \dotsc, x_n] \]

\(A x_i\)는 \(A\)라는 일종의 함수에 의해 선형 변형된 벡터를 나타낸다. 이러한 벡터를 모아 놓은 것이 \(AQ\)이다. 이는 벡터 (서브) 스페이스를 형성한다.

\[ Q \lambda = [x_1, \dotsc, x_n] \begin{bmatrix} \lambda_1& \dotsc & 0 \\ \vdots& \ddots& \vdots \\ 0& \dotsc& \lambda_n \end{bmatrix} \]

이것 역시 벡터 (서브) 스페이스를 형성한다. 여기서 서브 스페이스의 축은 아이겐벡터가 되고, 그 길이를 좌우하는 것은 아이겐밸류가 된다. 이렇게 살펴보면, 왜 아이겐벡터-아이겐밸류가 선형 변환 함수 \(A\)의 축과 크기를 바꾸는 것인지 이해할 수 있다.

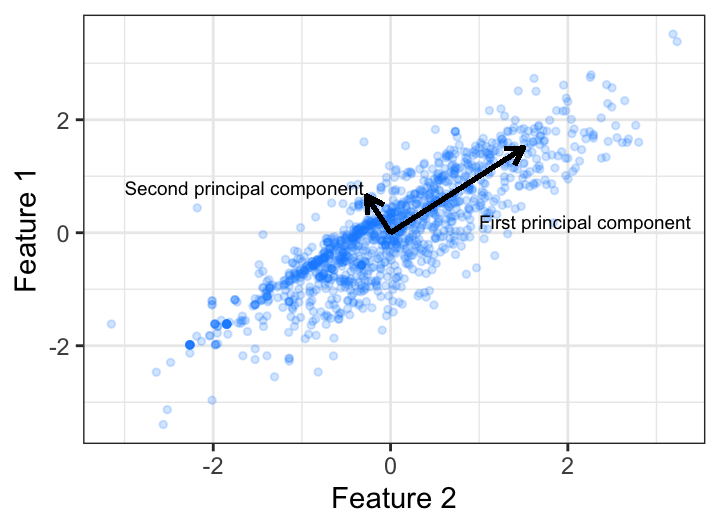
PCA를 예로 들어보자. \(x-y\) 축 위에 찍힌 점들에 대해서 변동성(분산-공분산 행렬)이 큰 방향으로 축을 바꾸면 어떻게 될까? \(x-y\) 축에서 보듯 축은 직교하는 것이 좋다. 그래야 두 개의 성분이 온전하게 쪼개진다. 위에서 보는 PCA의 새로운 축은 아이겐벡터의 방향을 중심으로 재정렬된 축을 나타낸다. 이 축에 할당된 변동성의 크기는 각각 축(아이겐벡터)의 길이에 해당하는 아이겐밸류가 된다.

참고

• Cherney, Denton and Waldron, 12.3 Eigenspaces, Linear Algebra.
• Boehmke & Greenwell, Principal Compnents Analysis, Hands-On Machine Learning with R